We've encountered in previous section Cartesians products of two sets, this time we will show that we can form something like the Cartesian product but of infinitely many sets, provided that the sets are suitably indexed.
Infinite Cartesian Products
Consider the following, a set I and a function H whose domain includes I. Now, for each i in I we have the set H(i); we want the product of the H(i)'s for all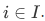 
This we write as
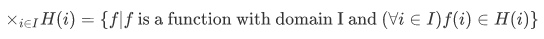
Thus we can say that the members of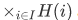 
are "I-tuples" for which the "ith coordinate" is in H(i). By "ith-tuple" we mean, (from section 3.3)
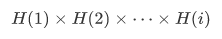
Example If for every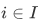 
we have 
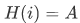for some one fixed A, then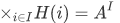 
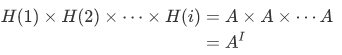
Example Assume that the index set is the set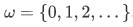 
. Then 
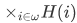consists of (i.e. functions with domain $\omega$) that have for their ith term some member of H(i).
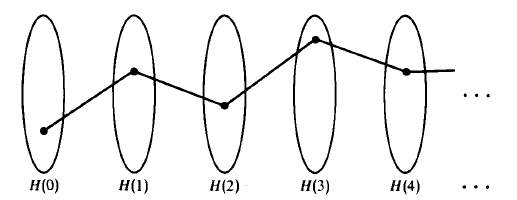
If we picture the sets H(i) as shown below, then a typical member of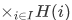 
is a "thread" that selects a point from each set.
If any one H(i) is empty, then clearly the product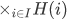 
is empty.
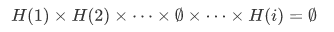
How about the converse, that is, suppose that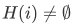 
for every i in I, does it follow that 
?
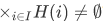To obtain a member f of the product, we need to select some member from each H(i), and put f(i) equal to that selected member. This requires the axiom of choice, and in fact this is one of the many equivalent ways of stating the axiom.
Axiom of Choice (second form) For any set I and any function H with domain I, if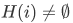 
for all i in I, then 
.
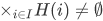Disclaimer: this is a summary of section 3.5 from the book "Elements of Set Theory" by Herbert B. Enderton, the content apart from rephrasing is identical, most of the equations are from the book and the same examples are treated. All of the equation images were screenshots from generated latex form using typora
Thank you for reading ...
