Elements of Set Theory: Notation

To denote sets, we will use a variety of letters, both lowercase (a,b,...), uppercase (A,B,...), and even script letters and Greek letters. Letters can be embellished with subscripts, primes, and the like.

It will be advantageous to exploit symbolic notations from mathematical logic. This symbolic language, used to replace the English language, has the advantage to both conciseness (shorter expression) and preciseness (less ambiguous expressions).

The following symbolic notations will be used to replace the following English language:

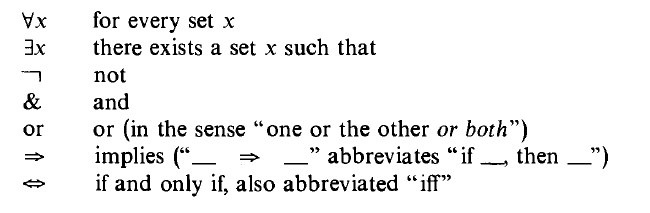
We also have available symbols for "membership" and equality namely: 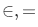respectively.

Wit all these symbols, variables, and parentheses, we could avoid the English language together in the statement of axioms and theorems.

Note that the $\forall{x}$ read as "for all sets x", rather the "for all things x". This is from the fact that we agreed to eliminate atoms from our theory. Everything we consider is a set; e.g., every member of a set will itself be a set.

Example:

1.Let's try to convert our "principle of extensionality" into a formal language:

Then "A and B have exactly the same members" can be written as

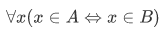
so the extensionality can be written as,

2.Another example, we will convert into a formal language is the following statement:

There is a set to which nothing belongs

This can be written formally as,

These two examples constitute our first two axioms.

^{Disclaimer: this is a summary of section 1.4 from the book "Elements of Set Theory" by Herbert B. Enderton, the content apart from rephrasing is identical, most of the equations are from the book and the same examples are treated. All of the equation images were screenshot from generated latex form using typora.}

Elements of Set Theory by Herbert B. Enderton

Thank you for reading ...