Ordering on Natural Numbers
Previously, we have defined natural numbers that was a side effect of our spurious definition, e.g. 
. Also, we have the following simple definition of order on natural numbers:
For natural numbers m and n, define m to be less than n iff
We then, introduce a special symbol "<" for this:
Note, this may seem redundant in a way that we can just use 
. But we have to keep in mind that the symbol "<" has a dual role which is to denote both membership and ordering.
Now, in place of an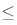 
symbol, we define
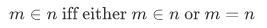
Observe that
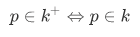
a fact we will use in later calculations.
We are now entitled to state the following fact:
any natural number is just the set of all smaller natural numbers.
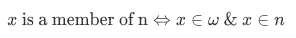
which is true because
is a transitive set, and thus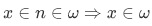 
Because each natural number is a transitive set, we have for m,n,p in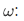 
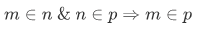
That is, our ordering relation on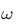 
is a transitive relation.
With this definition, it is hard to show that between two distinct natural numbers, one is larger than the other. For that, we need the following lemma,
Lemma 4L (a) For any natural numbers m and n,
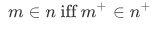
(b) No natural number is a member of itself
We next use the lemma to prove that for two distinct natural numbers, one is always a member of the other.
Trichotomy Law for set of natural numbers: For any natural numbers m and n, exactly one of the three conditions,
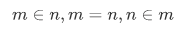
holds.
Disclaimer: this is a summary of section 4.5 from the book "Elements of Set Theory" by Herbert B. Enderton, the content apart from rephrasing is identical, most of the equations are from the book and the same examples are treated. All of the equation images were screenshots from generated latex form using typora
This post has received a 4.42 % upvote from @boomerang.
Congratulations @sinbad989! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
SteemitBoard and the Veterans on Steemit - The First Community Badge.
Congratulations @sinbad989!
You raised your level and are now a Minnow!
Do not miss the last post from @steemitboard:
Congratulations @sinbad989! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Congratulations @sinbad989! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Congratulations @sinbad989! You received a personal award!
Click here to view your Board of Honor
@tipu profit 1000 sp delegated
Yesterday 1000.0 STEEM POWER delegated or invested gave payout of:
0.042 SBD + 0.326 STEEM (0.15 USD), APR: 16.3% .
Delegation link: steemconnect 1000.0 SP delegation to @tipu.
Please note that your profit can be slightly different (depending on the payout time).Check out https://www.steemprofit.info to compare @tipU with other services.
@tipu profit 1000 sp delegated
Yesterday 1000.0 STEEM POWER delegated or invested gave payout of:
0.095 SBD + 0.279 STEEM (0.23 USD), APR: 17.62% .
Delegation link: steemconnect 1000.0 SP delegation to @tipu.
Please note that your profit can be slightly different (depending on the payout time).Check out https://www.steemprofit.info to compare @tipU with other services.