Elements of Set Theory: Ordering Relations

From the first section of this chapter, we've covered about the ordering relation of the ordered set

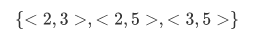
Now we want to consider the ordering relation on other sets. But first, we will deal with the basic concepts of ordering relations which we will find useful in chapter 5.

What, in general, should it mean to say that R is an ordering relation on a set A?

Basic instinct tells us that ordering relation is about determining given any distinct x and y which one is smaller.

Definition Let A be any set. A linear ordering on A (also called a total ordering on A) is a binary relation R on A (i.e., $R \subseteq A \times A$) meeting the following two conditions:

a) R is a transitive relation; i.e., whenever xRy and yRz, then xRz

b) R satisfies trichotomy on A, by which we mean the for any x and y in A exactly one of the three alternatives,

holds

Theorem 3R Let R be a linear ordering on A.

i) There is no x for which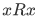

ii) For distinct x and y in A, either

This theorem is about the trichotomy conditions. A relation meeting condition (i) is called irreflexive while those relations satisfying (ii) is said to be connect on A.

Note that we cannot have a linear ordering R leading us to circles,

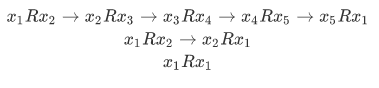
The transitivity is contradicting the condition (i) of the foregoing theorem. We can't have that in our linear ordering relation.

The commonly used symbol for linear ordering is not R but "<". For then we can write "x < y" which implies that the pair is related and a member of the set <.

Visualization of the Ordering

The members of set A can be represented by dots, with the rule that we place the dot x below the dot y whenever x < y. We add vertical lines to connect the dots. For an easy visualization consider the following figure,

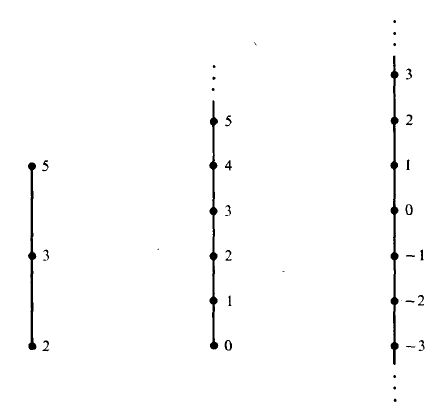
There are other important concepts of linear ordering but we will discuss them more in the first section of Chapter 7. We will encounter a "non-linear" form of the ordering relation,

^{Disclaimer: this is a summary of section 3.7 from the book "Elements of Set Theory" by Herbert B. Enderton, the content apart from rephrasing is identical, most of the equations are from the book and the same examples are treated. All of the equation images were screenshots from generated latex form using typora}

Elements of Set Theory by Herbert B. Enderton

Thank you for reading ...