Graph theory sounds hard, but the underlying concepts are pretty simple - and they can be understood without much math. Even better, once you grasp the fundamentals of graph theory, you will understand:
- How networks like Steemit (or Facebook, or Twitter) grow.
- What makes those networks strong or vulnerable.
- The role that you play in the network, and how you can change your behaviours to either suit your strengths or help out in the network's weak spots.
If you want to know how Steemit can scale from a small user-base to a genuinely mass-market phenomenon, and how you can help make that growth happen, then understanding graph theory is a must.
In this post, Part 1, I'll take you through the basics of graph theory and flag up the applications for a social network. In the next post, Part 2, we'll walk step-by-step through the growth of a Steemit-like social network, and you'll understand how to leverage the power of graph theory to build the platform.
both questions will get 10% of the SBD award for both posts. That could be 10% of $0, but you're here for the joy of learning, right?As an incentive to stick with me through the learning process, and because I'd like the #learning community to grow, there'll be a quiz question at the end of each post. The first person who gives me the right answer to
Let's get started!
Edges and nodes
A graph is a way of thinking about connectivity. To express that formally, you only need to understand two bits of terminology. A graph is made up of nodes (which can represent real-life objects like railway stations or users on a social network) and edges, which are the connections between nodes. To get a handle on the basics, let's look at a simplified train network, represented as a graph, where the train stations in six cities are nodes and the railway lines between them are the edges.

This looks like...well, pretty much any transit map you care to think of. And, in fact, if you have ever got on a train and counted the number of stops to your destination, then you already understand the concept of path distance.

The path distance between two nodes is simply the minimum number of edges you need to pass along to travel between them. The path distance between Portland and New York is 2, because our train travels two 'stops', or edges: Portland→Boston and then Boston→New York.
Network resilience
Maybe you notice a couple of things looking at this railway graph? Intuitively we might say that the graph is grouped into parts: the loop of four stations, from New York to Washington DC, and the spur that runs from New York up to Portland. And we might also think that the loop of stations looks more 'connected' than the spur. Later, we'll think about this more formally, but look at what happens when we remove the edge between New York and Boston (maybe the railway line is out for maintenance).

Noooo, someone broke our railway!
We now have one graph, but it is split into two components. A component is a set of nodes connected by some path or, to use our railway station analogy, stations that it is possible to travel between. Before we had a single component in our graph, because a path existed between each pair of nodes, but now it is impossible to travel between, for example, Portland and Baltimore.
Notice that, had we removed any one of the edges in the New York-Philadelphia-Washington-Baltimore loop, we would still be able to travel between any two stations, and would therefore still have one component in the graph. It is only by removing one of the two edges Portland-Boston or Boston-New York that we cut the graph into two pieces. This kind of edge is called a bridge.
Bridges are an important concept for understanding Steemit. In the railway example, bridges seem to be weak points in the network. If one line fails, then travellers can't get between two places - so it might be better to build in some redundancy.
But, as I'll show you in more detail in Part 2 of this guide, bridges are also crucial for network growth, and the nodes on either side of a bridge can wield great social power. Want to be powerful even though you're a Steemit minnow? Then work out your place in the network, and play to your strengths.
Connectedness
Right at the start, I told you that graphs are a way of thinking about connectivity. The simplest measure of connectivity for a single node is its degree: the number of other nodes that it is connected to. In our original railway graph, the degree of New York is 3 because it is connected to three other stations (Boston, Philadelphia and Baltimore), while the degree of Portland is 1 because it has a single connection (Boston).
If we scale the size of the nodes based on their degree, the plot of the railway graph looks like this:

In a social network like Steemit, being connected makes you, and your actions, important. The insight that connection is a proxy measure for authority is what lies behind Google's PageRank algorithm. We'll find out more about how powerful connections drive network growth in Part 2 of this guide.
Centrality
In case you hadn't figured it out already, the simple structure of nodes and edges generates a lot of complexity and interesting behaviour. One of the most important questions for people interested in networks is: which nodes are important? In a social network like Steemit, who are the whales and who are the minnows? In a transport network, what differentiates a busy hub from a disused backwater station?
There are many ways to measure the centrality, or importance, of nodes in a graph. I'll show you one for now.
Closeness is (roughly speaking) a measure of distance. It is the inverse of the sum of path distances to each other node. So, for New York, the closeness measure is:
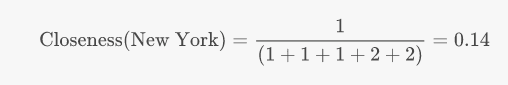
The table below shows the closeness measures for all of our stations. It also shows the betweenness centrality - this is a measure of how often a node acts as a bridge between other nodes. It is an important gauge of social power in a network, and we'll talk more about it in Part 2 of the guide.
| Station | Closeness | Betweenness |
|---|---|---|
| New York | 0.14 | 6.5 |
| Boston | 0.11 | 4.0 |
| Philadelphia | 0.11 | 1.5 |
| Washington DC | 0.09 | 0.5 |
| Baltimore | 0.11 | 1.5 |
| Portland | 0.08 | 0.0 |
As this table shows, New York wins on measures of closeness and betweenness - and it has the highest degree.
Conclusion and quiz question 1
In the next part of the guide, I'll go through the process of how a network grows - using Steemit as an example - and the different roles that users play in that process. My goal is to show you that understanding graph theory will help you become more like New York and less like Portland.
If you want to see how I made the diagrams for this post, all the R code is in this repository.
Quiz question 1:

The plot above shows a graph representing friendships between 8 people. Which node has the highest degree and what is the degree?
Remember, the quiz is in two parts, so don't post your answers just yet.
Cool, looking forward reading it ... thanks
This is great though would be nice to hint more about where you are going with it. What is your background?
Thanks - my academic background is in history, but then I taught myself programming and stats, and now do freelance data science/analytical stuff. (If that seems weird, historians really care about data quality.) Network analysis like this is probably my favourite area because there are so many real-world applications for something that has a lot of theoretical depth - plus, cool visualisations!
10 cents and i was 8 of them makes me want to cry
I think part 2 will be better. Stick with it then part 1 will also gets votes. People will like it bttes( read whales) if it helps them plan strategy to expand network. That sounded like part 2. Which nodes are the "closest" to expand to. I say politics finance and academic economics. Cryptocurrency people are all interested in these topics. These are there closest next cities.
Also posts next one under marketing.