So, I must admit, I am really geeking out this week over some of my favorite math tricks.
It is so much fun to have a community where sharing such things is truly appreciated. And, it is especially fun when reading a bunch of different pieces inspire you to do even more.
I've been thinking about writing this for a while, but was dragging my feet because I didn't want to do all the applet creating nonsense. But, it's Saturday, and I'm in between tasks. So I humbly submit to my fellow Steemians an awe inspiring mathematical trick:
How to Generate Pythagorean Triples
What is a Pythagorean Triple you might ask? Well, as I also mentioned in the title of the article, it is any set of three integers that satisfy the Pythagorean Theorem. Namely, three non-decimal numbers a, b, and c that satisfy:

Many of us tend to memorize our favorite sets of triples based on problems that tend to pop up in textbooks over the years. For instance, (3, 4, 5) always satisfies the Pythagorean Theorem. So does (5, 12, 13). Literally useless knowledge I will never forget because I've seen so many problems with these particular combinations.
If you've advanced farther in mathematics, you may have even learned that any multiple of a Pythagorean triple is also a Pythagorean triple. So, (6, 8, 10) = 2*(3, 4, 5) should also satisfy the Pythagorean Theorem.
But, what about other cases? Is it easy to generate any (a, b, c) that satisfy the Pythagorean Theorem? It is a question I'm sure you never wanted to ask, but believe me, you do. It is just SO MUCH FUN to investigate!
Part 1 - Guess and Check
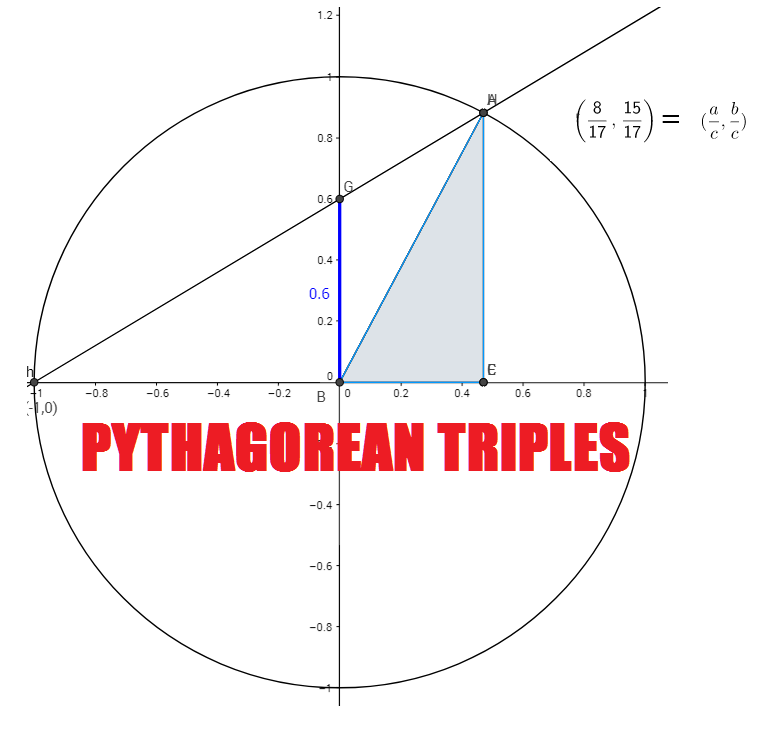
Okay, here is the dirty secret about the Pythagorean Theorem. All of its values can be generated from a circle of radius 1. Or, what math dorks like to call the unit circle. Why is this, exactly? Check out the following:

With a clever substitution of  and
and  , you have the equation of a circle with a radius 1:
, you have the equation of a circle with a radius 1:

So, on this circle the logic follows thusly -- Any coordinate (x, y) must be a coordinate that satisfies the Pythgorean Theorem. Awesome! And, it just so happens, the particular coordinate must be a fraction with a, b, and c all having roles in their construction.
Try it out for yourself! I made an applet using Geogebra where you plug in values for a, b, and c. If it satisfies the Pythagorean Theorem, you should see a triangle appear on the circle with the vertex A intersecting the circle . If it does not, you will see a triangle with vertex A off of the circle.

Part 2 - Getting Smarter
So, the above was cool, but it was just guessing and checking. What if we could algorithmically find all these rational (x, y) coordinates without having to always guess their value?
We can so do this!
Here's what we can do.
- Create a line that passes through the points (-1, 0) and the circle at (x, y).
- This line will create two similar triangles. One is formed by the sides y and (x + 1), the other by what I will call t and 1.
- Since we constructed both to be of the same slope, we can equate their slopes and get a really nice result for the value t:

- Now we can solve for x! We just need to solve the circle equation for y^2 and substitute the circle equation into the equation we just found for t:

- Great we have x!
- Now to get y, we back substitute what we just found for x into our original formula for t:

- This always means that, for a unit circle of radius 1, any value t will satisfy the pythagorean theorem with rational coordinates of:

Math Rocks!
Check all this playing out below on the interactive applet I've made for you below. Again, we have the unit circle and this time we have a slider for t. Obviously, since this circle is of radius 1, the largest we can have t go is 1.
Play around on the slider, does every value generate a Pythagorean Triple? It very well should! But, feel free to check in the input boxes below. If it does the red unit circle triangle should overlap with the newly defined blue one.

Huh? Why does this work?
Because it satisfies the Pythagorean theorem, fam!

What about if the circle does not have a radius of 1?
Well, all we would need to do in the steps above is to replace any value of 1 with another constant value, like p. Yes, I picked p so below would have t and p in it. I enjoy toilet humor.
Trivially, with radius of value p, our formulae would work out as follows:

Again, this would indeed satisfy the Pythagorean Theorem. We would just be careful to pick a value of p that is larger than t so we don't get a negative value for a.
I thought you said this was "Pythagorean Triples Made Easy"????
Okay, well we are finally here! We 👏 have 👏 our👏 formula!👏
We can take any integer t and p and make out of it a Pythagorean Triple. Let's take it for a spin:
- (ex) t = 3 , p = 7 would generate the following Pythagorean Triple:

Does it work?
You bet your sweet Pythagorean Behind it does! The fractions just reduce.

So, next time you are on a date, or just want to impress your family or friends, do I have the line for you!
"Give me two numbers, any two numbers. I will turn them into a right triangle"
Steemit Board Awards - Click Below for More Information





Am glad you're enjoying your comeback! It makes a difference now that there is a growing audience :-)
And for the newbies, here's the sig......
!!!=o0o=!!!
you then read this article.
Click here for Mathematics forum on chainBBTo follow curated math content follow @math-trail. If you wish @math-trail to follow
Wow! He had right when he said: 'There is nothing so easy but that it becomes difficult when you do it reluctantly.'
I suppose so ;)
This is awesome, nice work!
Thanks! It was a lot of fun to put together. I always love making Geogebra demonstrations, they are just such a pain...especially when they don't upload like you want them to. Glad you enjoyed!
Well I'm grateful you endure the painstaking process to upload your work for us to enjoy and learn from, hehe.