This article talks about Merkle Tree and Merkle Root. The concept is used in many blockchains, for example in the Ethereum or Bitcoin blockchain. Merkle tree is often mentioned when talking about blockchain, Bitcoin or similar topics. Hence it is useful to know what a Merkle tree is

The article is part of a series starting with this article: Blockchain Foundations Part 1: Distributed, Decentralized and Centralized Computer Architecture

The articles are drawn from my book "Blockchain and Crypto Currencies Easy to Understand for Everyone, Thomas Bauer". Please refer to the part 1 article for a introduction to the blockchain foundations series.

Merkle Tree and Merkle Root

The Merkle tree is a hash tree. Ralph Merkle specified it in 1979. It is a tree consisting of hash values.

All leaves of the tree represent the hash values of data blocks
All intersections of the tree represent the hash value derived from 2 to n subjacent hash values. In a binary hash tree an intersection hash value always is derived from exactly 2 subjacent hash values

For building the Merkle tree in the subsequent example in the first step of all strings (like "A sends 0,01 BTC to C") on the lowest level the SHA-256 hash value was derived. To build the nodes the hash value for each node was derived from the concatenated two hash values below the node.

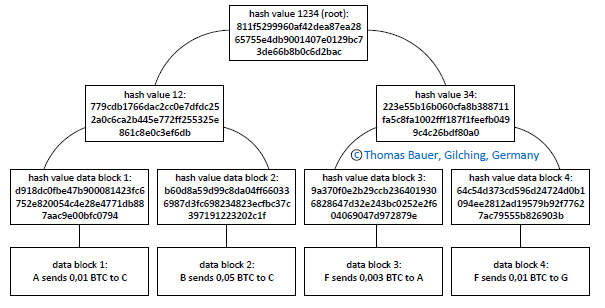
Figure 5: Merkle tree

What to do if there are not exactly 4, 8, 16, … transactions? There are different methods. One method for a node with only one leave is to duplicate the existing leave. That is the way Bitcoin does it.

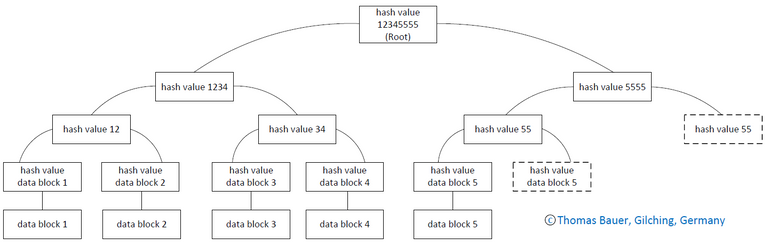
Figure 6: Merkle tree with an uneven number of leaves

We use the Merkle tree to check data blocks being unchanged since they have been stored. For this we only need to store the root hash value. A new calculation of the Merkle tree bases on the stored data blocks will lead to the same root hash value, if the data blocks are unchanged.

With a Merkle tree we can check data blocks with little costs. Assume we want to check data block 4 shown in the figure above for being unchanged. Then we need for the check beside data block 4 and its corresponding hash value only the hash value of data block 3, the hash value 12 and the hash value 5555. The hash values 34, 1234 and 12345555 we calculate from these inputs to check for data block 4 being unchanged.

If we add a new data block to a Merkle tree, we do not need to recalculate the whole tree. We only need to recalculate the hash value of the new data block and the hash values of the nodes above the new data block. Then our Merkle tree is consistent once again.

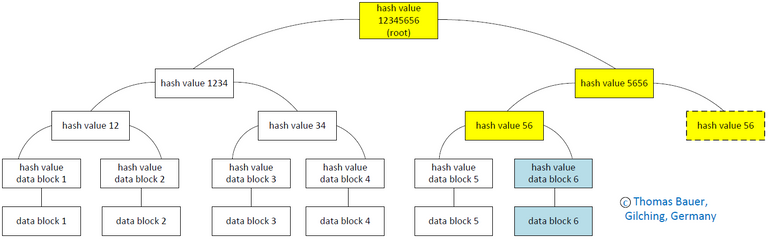
Figure 7: Do a change to a Merkle tree

In the figure the light blue elements (data block 6 and hash value data block 6) where added and calculated. The yellow elements (hash values 56, 5656 and 12345656) we need to recalculate. All the other elements with the white background remain unchanged.

Blockchain uses Merkle tree for example for:

For storing the transactions within a block as Merkle tree
Bitcoin calculates a hash value for each block. Because the transactions are stored in a Merkle tree the Merkle root hash value represents all transactions in the block. Hence for the calculation of the block hash value it is not necessary to derive a hash value from all the data contained in the block. It is enough to derive the block hash value from the block header containing the root hash value of the Merkle Tree

Merkle tree is often mentioned when talking about blockchain, Bitcoin or similar topics. Hence it is useful to know what a Merkle tree is. On the other hand, Merkle tree is located deep in the details of implementation. You will understand blockchain without knowing details about the Merkle tree or even knowing how to build one. It is enough to know that a Merkle root hash can unambiguously represent the complete data structure it stands for.

Blockchain Foundations Part 5: Merkle Tree and Merkle Root

Merkle Tree and Merkle Root