This is part one of a summary I am writing for the paper "A primer on encoding models in sensory neuroscience" by Marcel A.J. van Gerven. Today's post is on chapter 1.3.
Defining x(t), a(t) and y(t)
Encoding consists of mapping sensory stimuli to neural activity or, more accurately, measurements of neural activity.
The sensory stimuli can be thought of as a vector x. For visual stimuli, each entry could be the intensity of a pixel for example. We call x the input vector. x(t) equals the input vector at time t.
If we separate the brain into p distinct neural populations, we can think of neural activity as a vector a with an entry for the aggregate neural activity in each population. a(t) is the neural activity at time t.
We can't measure neural activity directly, though. Instead, we make measurements from sensors. A sensor could be a voxel in an fMRI scan for example.
If we have q sensors we can put all our measurements into a vector y with q entries. y(t) is our measurements at time t.
Lets redefine our problem
Instead of choosing a specific encoding for our stimuli, we could calculate a probability distribution. A probability distribution is a tool we can use to ask questions like, "Given this sequence of input vectors {x(0), x(1), ...}, what is the probability we will make these measurements {y(0), y(1), ...}?".
In other words, we can describe an encoding model as a mathematical framework for quantifying which measurements are likely depending on the stimuli. Using an encoding model to make predictions about measurements is how neural encoding is implemented in practice.
In order to calculate the probability distribution we need to understand the relationships between x(t), a(t) and y(t).
y depends on a depends on x
Let's first quantify the relationship between x(t) and a(t). We know that, somehow, a(t) must depend on x(t) because neural activity reacts to outside stimuli. a(t) can then influence future activity when the brain continues processing the information. Another way of saying this is that the current neural activity not only depends on the current stimuli, but also on the previous neural activity.
We can write: a(t) = g(x(t), a(t-1)) where g is some nonlinear function.
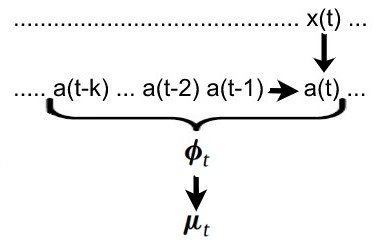
We have a similar situation when defining the relationship between a(t) and y(t). Due to lagging and other signal-altering effects, y(t) depends not only on the current neural activity a(t), but on the "history" of neural activity.
For brevity we can call the history (a(t), a(t-1), a(t-2), ... , a(t-k)) the feature space phi(t). Each entry can be calculated with g. (see above)
Since we are dealing with probabilities, we don't calculate the measurements from the neural activity directly. Instead we calculate the expected value.
mu(t) = f(phi(t)) where mu(t) is the expected value of y(t) and f is called the forward model.
You can think of the forward model as a function which calculates the most likely measurement given the feature space. In other words, f maps a history of neural activity to the likeliest resulting measurement.
Conclusion
Now that we understand how to calculate the expected measurement vector mu(t) from the input vector x(t), we need to put everything together to get a probability distribution. That will be the topic of the next post.
Congratulations @trilo! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPLet me ask a few questions to make things more concrete. Are the following correct observations from your proposal statement?
If we were studying visual processing, the matrix x could be implemented as an m x n 2-D matrix, where each element of the matrix corresponds to a grayscale value in a digital photograph of the object that the subject brain is observing. The size of the photograph is m values by n values.
To capture color, we could create three such matrices, where each contains the values from one channel in an RGB image. So the first matrix contains the red values, the second contains the green values, and the third represents the blue values.
Are these correct assumptions about x, or did you have something different in mind?
Is that a correct assumption? So if the subject started to smell the aromas of a heated lunch wafting in from a nearby break room, this should theoretically have no impact to the values in a. Is that right? If not, how would you handle that?
The fMRI that gives rise to the values in matrix y is a three dimensional picture of the brain. How would you propose to represent those values? Would each slice of an MRI scan (a 2D image) populate pixel values in separate matrices, y1, y2, y3, et cetera?
It takes a long time to take an fMRI of the entire brain (let's say something like 10 minutes). I'm assuming that the timestamps of each MRI slice are not what you had in mind for the t time parameters for a, or are they?
Is there any way to mask the fMRI data such that it excludes neural activations not relevant to visual processing (e.g., smelling cooked food, feeling pain from arthritis in one's neck or back while laying on the lab table, auditory cues from the MRI machine making noise)?
Thank you for these questions! They motivate me the write more.
Well fMRI is pretty crappy, but it isn't THAT crappy. https://en.wikipedia.org/wiki/Functional_magnetic_resonance_imaging#Temporal_resolutionThanks. I hope some of it was beneficial. The devil is usually in the details on projects like this, so the sooner you can confront potential traps, the better.
Re: matrices versus vectors: I tend to use the term "matrix" more since I always keep the numbers in that form until a matrix multiplication operation is required, then I unroll and roll the matrix as needed to use the optimized multiplication algorithm.
Re: colors: If the inputs to the CNN are photos of real world objects, I would go with the multi-channel approach, because it's the closest thing to be inspired from biology. We have separate cones in the eyes for reds, greens, and blues, while other living organisms have even more diversity, adding cones from UV light and polarized light (useful for seeing underwater). If the retinal neural cells combine the inputs from the different cones, that's one thing, but I don't think they do. That said, I think the situation changes if the inputs to the CNN are fMRI images. Don't they basically contain false colors to indicate some level of intensity? If that's the case, I would expect grayscale encoding to work.
Re: temporal characteristic of fMRI data: I was just going by personal experience. I underwent a brain MRI scan once, and it took 10 minutes. But the stats on the Wikipedia page you cited doesn't give me much confidence. I suspect that current techniques are not capturing a large amount of neural activations.
Re: filtering out neural activations in the fMRI image that represent undesired sensory inputs: I understand your response, but just be aware that this might be a matter of relevance, not noise. If the noise follows a particular pattern, the CNN may wrongly incorporate that pattern into its predictions. Think of the old experiment that classified tanks from cars, and failed, because all the photos of cars were taken on sunny days, and all the photos of tanks were taken on cloudy days. The CNN in that experiment started focusing on the sky color as a feature, rather than treating it as irrelevant data. It wasn't noise from the classic sense (from information theory and communication channels), because it was deterministic and not random (although that was an unfortunate coincidence). From another perspective, this problem seems a lot like an NLP experiment that attempts to separate simultaneous conversations at a party where a number of microphones scattered among the crowd are recording voices.
Incidentally, a Kaggle competition from a while ago used brain fMRI data. It might be useful to track down the winner of that competition and ask about the approach he or she took.