
To achieve nuclear fusion on Earth creates a lot of challenges. In this post I’ll explain some of the barriers that have to be broken in order to thrive.
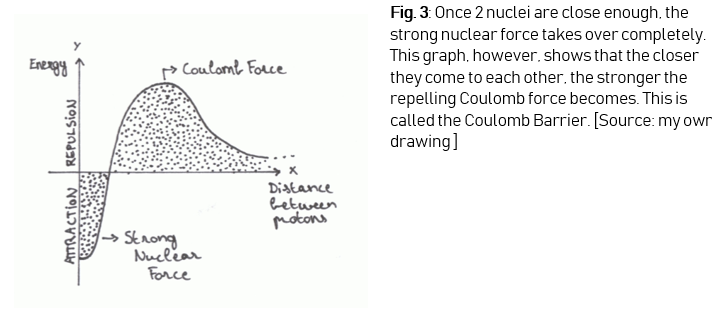
To fuse 2 atoms together a lot has to be taken into account. In a plasma, atomic nuclei and electrons are separated. If 2 atomic nuclei come close to each other they repel – a consequence of the Coulomb force or electromagnetic force, one of the 4 fundamental forces of nature. This force makes particles with the same charge repel each other. There is a second force on the other hand, and this force makes fusion possible. If 2 nuclei come close enough, they seem to stick to each other. The force that allows this to happen is the same force that makes quarks as well as neutrons and protons bind with each other – the strong nuclear force, another fundamental force of nature. This force creates nuclear
attraction, but it only works if 2 nuclei are close enough
to each other (Figure 3).
In order for 2 nuclei to come close to each other, they need a lot of kinetic energy. We know that the kinetic energy of particles equals the temperature of a system, so the system needs to be heated up to extreme temperatures. If we calculate the amount of energy needed to overcome the Coulomb Barrier, a problem arises.
Calculation of the amount of energy needed for deuterium-tritiumfusion:

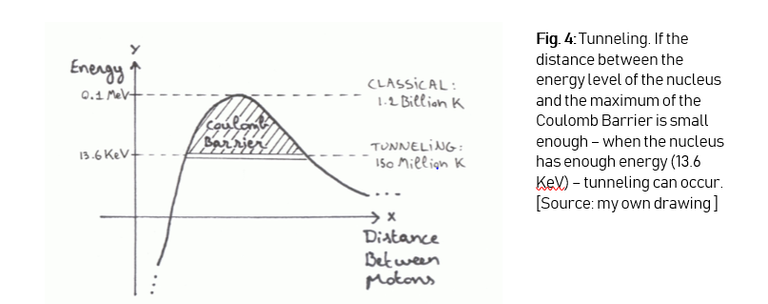
After putting in the right values in the equation, we get an energy amount of 0.1 MeV. This is an enormous amount. To put it in perspective: we would have to heat the gas to 1.2 billion kelvin, which is impossible in this stage of technological advance. But we know that nuclear fusion IS possible, and this is because of 2 things:
First we have the duality principle, this allows particles to undergo a quantum mechanical effect called tunneling. We’re not going to go into the details of quantum tunneling, but the things you have to now are depicted below (Figure 4). The process of tunneling plays a big role in nuclear fusion, on earth as well as in the sun. It’s because of this effect that in deuterium-tritiumfusion, a particle needs about 13.6 KeV of energy, which translates into a temperature of about 150 million degrees (I make no distinction between kelvin and degrees, because at these extremely high temperatures it doesn’t really make a difference).
Secondly, the temperature we calculated is an average temperature. If we look at the Maxwell-Boltzmann-distribution of hydrogen nuclei at a given temperature T, we can see a long tail of highly energetic particles. These particles have a much higher shot at achieving fusion (Figure 5).

As you might know, the sun’s core only has a temperature of 15 million degrees, and still nuclear fusion occurs. There are 2 reasons for this. The first one is that the pressure that rules in the sun’s core is impossible to create on earth. Because the sun is so massive, the gravity is so strong that it creates enormous pressure in the core. This extreme pressure results in a lot of collisions between nuclei because all the particles are packed together, there’s a higher concentration. This, of course, creates a higher possibility for fusion to occur. The second reason is the amount of particles in the sun. Although the chance for nuclear fusion to happen is still extremely low, there are so many particles in the sun’s core that it still generates enough energy.
Thanks for reading guys! This was the second post of my thread on nuclear fusion. Many more to come! If you found this interesting, upvote!
(In your case, some references would be great. Good luck!)
(And try not to double post)
(and join steemit.chat and our group, #Steemstem)
Yes, thanks for the information. My plan was to include all my sources at the end of the thread. And also, I get these broadcasting errors when I post, and then when I check again it seems as if it posted twice or even thrice. But I've learned now, won't happen again!
cool cool, emphasis on joining us in the steemit.chat community!