
Now, we use the time-dependent Schrodinger equation to find the time rate of change of the probability density.
What is the probability density again?
Answer: 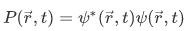
Probability Current Density
In thi section, we will calculate the time derivative of the probability density but first lets introduce the time-dependent Schrodinger equation and its conjugate equivalent.
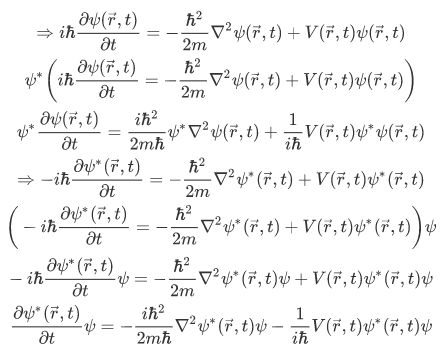
The time derivative of the probability density then with the aid of the equations above is given by,

We find that,
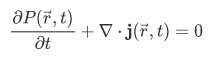
This is the continuity equation for the probability density. Here we have assumed that

That's it. We found the probability-current density. This describes the flow of the probability in terms of probability per unit time per unit area.
You got a 9.98% upvote from @dailyupvotes courtesy of @pauldirac!
This post has received a 21.88% upvote from @lovejuice thanks to @sinbad989. They love you, so does Aggroed. Please be sure to vote for Witnesses at https://steemit.com/~witnesses.