Imagine we have a cube and a sphere at the top of a inclined plane, as in figure. Suppose the plane have no friction
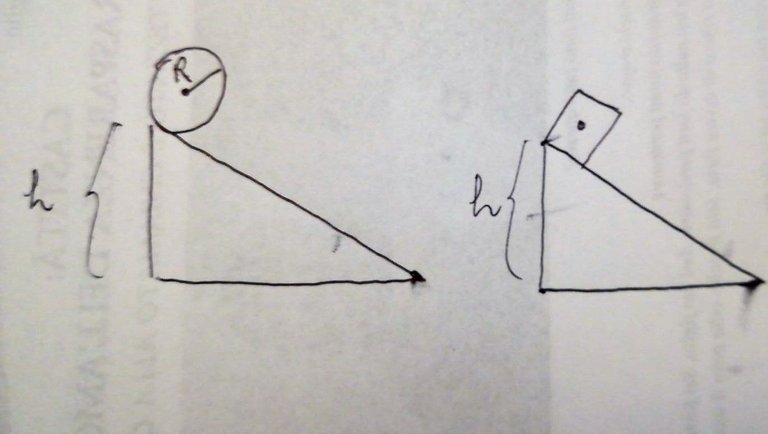
where h is the height of the plane, R is the radius of the sphere
Which of the two objects will travel faster at the end of the plane?
Obiousvly, the sphere. Sure?
To calculate the velocity of the two objects we can use the conservation of energy.
All the potential energy at the top of plane is transformed in kinetic energy at the end of the plane.
For the cube
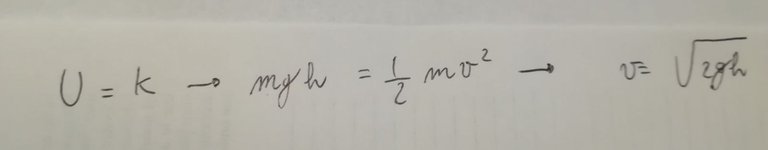
Simple.
To calculate the velocity of the sphere we must consider that we have two type of kinetic energy: traslational (as the cube) but also rotational
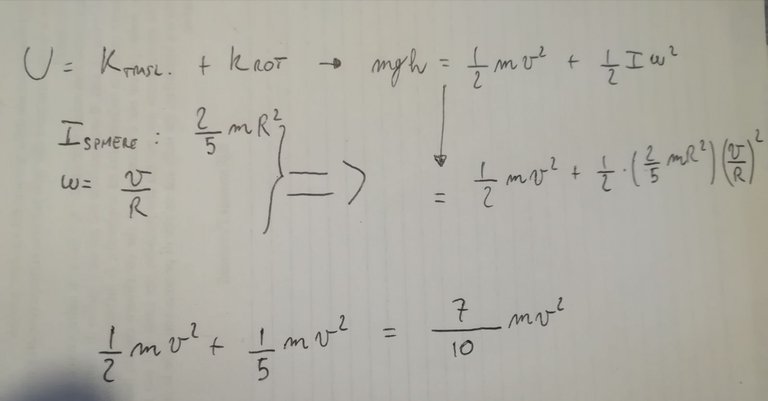
where I is a costant, depending on the shape and the mass of the object. For a sphere is 2/5 mR^2
and w (omega) is the angular speed.
Now we have the energy of the sphere expressed by a equation where we don't know just "v"
Conservation of the energy :)
.jpeg)
As you can see from the picture, the speed of the sphere is lower than speed of the cube (more or less 84%)
Ciao!
I don't agree u didn't figure in friction
This trick is based on "suppose the plane have no friction" ;-)
By the way, nice trick ;-) Do you know what is actually "I" constant means?
You have to forgive me, I don't speak english very well. "I" is the moment of inertia.
If really the plane would not have a friction the sphere would not rotate. I supposed that the sphere spins without crawling, in this way friction's work is equal to zero, but is the friction that allows the ball to rotate.
We have to think at "a little friction" that doesn't change significantly our hypotheses
Indeed, this difference in meaning is subtle but important
Ah.... Physics
if it has no friction... what makes the sphere "roll?" with no friction it would just slide down the ramp the same as the cube... 8)
You're right
I wrote it in a comment above ;)