In this article I want to tell you what Fibonacci numbers do, and why they are so useful as they have numerous applications and they are even used by our Nature that controls the growth of leaves in plants and even some galaxies have a spiral shape that obeys the Fibonacci law! People use this numbers in trading, programming, and different mathematical calculations.

Fibonacci numbers are elements of the numerical sequence. Each next number in the series is constructed as sum of the two previous numbers.
EXAMPLE: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ...
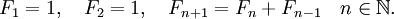
If we divide each next number of this unique sequence on the previous one, we will gradually come closer to some amazing transcendental ratio - F (Fibonacci number) = 1.6180339887
If we square any Fibonacci number, the result will be equal to the number standing in order before him, multiplied by the number that is behind it, plus or minus 1. For example, five squared is equal to 3x8 + 1; 8 squared is equal to 5x13 minus 1 and so on. The signs "plus" and "minus" changes alternately.
If we take two consecutive pairs of series and divide a greater number on the smaller, the result will gradually approach to the golden section.
Fibonacci numbers are calculated using the recursion. For a number n > 2 n-th number is equal (n - 1) + (n - 2).
Fibonacci numbers are often used in programming and they are the greatest example of recursion that could be written in Python just like this:
fib = lambda n: fib(n - 1) + fib(n - 2) if n > 2 else 1
Golden Section – is a division of integer on those parts which correspond to the following principle: a large part refers to the small as the whole part refers to the large part.
Described approximately, the golden ratio is a proportional division into two unequal parts: approximately 62% and 38%. The golden ratio is the number 1.6180339887 in numeric terms.

The length of the segment c = 1, a= 0,618, b = 0,382.
The ratio of C to A = 1, 618.
The ratio a b = 2,618
Let’s take two consecutive numbers of this order. Divide the larger number by the smaller and we get about 1,618. And now we use the same greater number and the next number - we get 0.618.
And in order to calculate the entire number of the Fibonacci numbers, we should know only three numbers of the sequence, coming one after the other.
Golden Rectangle and the Fibonacci spiral
Another interesting parallel between the Fibonacci numbers and the golden section allows drawing the "golden rectangle": its sides are related in a ratio of 1,618 to 1.
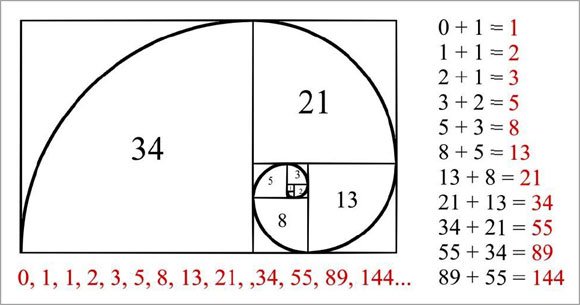
And then we divide large rectangle into smaller ones. Prerequisite: the length of the sides of the rectangles shall correspond to Fibonacci numbers. Those. larger rectangle side length must be equal to the sum of two sides of the smaller rectangles.
If you connect the corners of rectangles with a smooth line, we obtain a logarithmic spiral. Rather, a particular case - the Fibonacci spiral.
In conclusion I want to say that there are a lot of different uses ot this numbers in our life:
• The grow of leaves in plants - the distance between them is correlated with the Fibonacci numbers (phyllotaxis);

• the location of the scales of pine cones;
• flower petals;
• pineapple cell;

• The ratio of the lengths of the phalanges on the human hand (approximately), etc.
• Clamshell - one of the most striking examples. Moreover, some galaxies that can be seen from Earth have the spiral shape.
• Curiously, the DNA spiral is subject to the rule of the golden section - appropriate pattern can be seen in the intervals of its twists.
Trading
Fibonacci retracement is a popular and effective technical tool used by most traders to analyze market conditions and determinate potential important technical levels, which could influence the price movement.
Only a few parameters are practically used - correctional Fibonacci ratios - 23.6%, 38.2%, 61.8%, 76.4% and 100% which indicate the levels of support and resistance of the asset price.
Of course, there are a lot more applications of these mysterious numbers that are not covered here, but I hope this article get you a general idea on this mathematical concept.
Follow me, to learn more about popular science, math and modern technologies
With Love,
Kate
Ahhhh this takes me back, can barely remember any of this. Are you still at university or post graduate?
Currently, I'm a bachelor student. I hope the article reminded you of the University years)
Nice one. I actually had no idea about this property: :-)
"If we square any Fibonacci number, the result will be equal to the number standing in order before him, multiplied by the number that is behind it, plus or minus 1"
Thanks for the feedback.
I'm pleased you learned something new from the article.