El hombre es contradictorio por naturaleza, ya lo dijo Whitman; la época actual ha llevado esa naturaleza contradictoria a un extremo. Por alguna razón, que quizás un sociólogo pueda explicar mejor que yo, el hombre de hoy tiene una profunda crisis de fe en sí mismo. No de otra manera puede explicarse el inusitado éxito en ventas de ese género "literario" que se ha conocido como autoayuda, sustantivo que de suyo es discordante, pues el prefijo auto se contradice con el hecho de que se trata de una búsqueda definidamente externa de solución a problemas reales o inventados. No solo la autoayuda ha florecido: también la religiosidad exacerbada (no hay grupo guasap en el que no circulen estampitas tipo escapulario) y esa forma decadente de misticismo, que convierte la maravilla de lo aun no explicado en una vía de culto semirreligioso. De esta suerte es el correr parejos de términos como astrología y curación cuántica, sea lo que sea que esta última cosa signifique. En todo caso, cualquier fanático de Adriana Azzi venerará por igual a Deepak Chopra y, posiblemente, viceversa.
Aludo a una contradicción, pero aun no la he explicado. La ciencia actual descansa sobre los mismos supuestos racionales que la levantaron en los siglos XVII y XVIII, pero algunas de sus conclusiones son chocantes al sentido común. Allí está la gran veta de los "místicos", palabra para la que no consigo mejor manera de ironizarla que con las comillas. Se hace "misticismo" a partir de lo mal aprendido o enseñado. De allí cosas como la curación o sanación cuántica, absurda manera de deformar un conocimiento tan sólido y productivo como la física cuántica. La actitud no es nueva. La robusta matemática que legó el pitagorismo del siglo V a. C. venía acompañada de absurdas creencias que atribuían a los números características humanas o divinas. Por allí empezó la cosa. Pero sorprende que a 1600 años de distancia la humanidad aun no sepa distinguir el trigo de la paja. Y que sea esta última la que brote de la boca de muchas personas, no solo con naturalidad, sino también con impostora autoridad.
Empujan estas reflexiones uno de los tantos vídeos sobre la materia que uno consigue por Facebook. Alude éste a los "misterios" del 9, partiendo del "enigmático" hecho de que la circunferencia tiene 360 grados y que 3+6+0=9. A partir de allí se enuncia una lista de "insondables" de la misma naturaleza. Pero dejemos de lado la ironía y veamos que tan insondables son las cosas que nos muestra el vídeo. Comencemos por decir que manejamos los números con un sistema posicional y de base 10. Son dos cosas: posicional significa que los dígitos con los que escribimos los números tienen valor de acuerdo a su posición, así en 666 el primer 6 es 600, el segundo 60 y el último 6. (¡No es nada diabólico, chico! El 6 fue lo primero que se me vino a la cabeza.) Por su parte, de base 10 o decimal (es lo mismo), significa que solo necesitamos diez símbolos diferentes para representar cualquier número y los indios nos regalaron estos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, con los cuales hemos estado muy conformes y cómodos desde finales de la Edad Media.

Fuente
Ahora bien, ¿es necesario que todo sistema posicional sea decimal?... Rotundo NO de respuesta. La única razón parece ser anatómica: tenemos diez dedos y nos iniciamos con ellos en el conteo. Por eso a los números de la lista anterior los llamamos dígitos, palabra que viene de dedo. Pero supón -haz el esfuerzo, lector- que en vez de diez tuviéramos ocho dedos, como la familia Simpsom. Ese simple detalle podría habernos conducido a otro sistema de numeración, uno de base 8, lo que hoy llamamos octal. En ese sistema los indios, de seguro, nos habrían dado solo ocho dígitos: 0, 1, 2, 3, 4, 5, 6, 7. ¿Y cómo seguimos aquí la secuencia? Pues... igual: al llegar al dígito más alto, rotamos de nuevo al 0 y empujamos las cifras a la izquierda, como el contador de kilómetros del carro:
0, 1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 13, 14, 15, 16, 17, 20, 21, 22, etc.
Pero, por supuesto, a pesar de usar símbolos comunes ya las cosas no significan lo mismo. En el hipotético mundo de ocho dedos, un corral de 12 gallinas significaría esto


(Los matemáticos expresan el hecho anterior dicendo que 12 octal es igual a 10 decimal y, como es de esperarse, muestran cómo una cifra octal se puede escribir de manera decimal y viceversa. No tenemos por qué entrar en ese embrollo, pero saludo a los lectores curiosos.)
Esta sería nuestra tabla de sumar si usáramos el sistema octal:
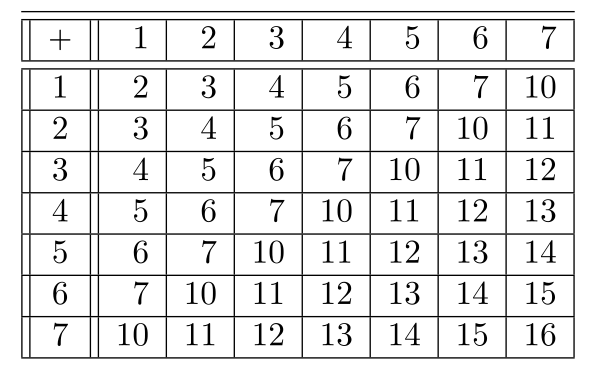
significa lo mismo, pero escrito de manera diferente. Te invito a descifrar.
Volvamos ahora al 9 y sus supuestas propiedades mágicas. En el sistema decimal, el 9 es el mayor dígito, pero en el sistema octal se escribe como 11 de manera que ahora se expresa con dos dígitos. En otras palabras: ser el mayor dígito es un acidente derivado de la base del sistema posicional usado, no da ningún privilegio a ningún número. Pero continúo: si te molestaste en ver el vídeo lo primero que notas es que la circunferencia tiene 360 grados y eso -según el autor del vídeo- no es casualidad. Pues... ¡sí que lo es! Si yo quisiera que la circunferencia tuviera 500 o 192 grados simplemente la dividiría en 500 o 192 partes iguales y a cada una la llamo grado. ¡San Seacabó! Lo que pasa es que hemos convenido desde hace mucho tiempo en 360 porque es un número que tiene una gran cantidad de divisores y además es una buena aproximación a la cantidad de días en un año, es decir, al tiempo que tarda la Tierra en dar una vuelta alrededor del Sol.
El otro punto en el que se solaza el vídeo es que 3+6+0=9, pero si divido la circunferencia en dos queda 180 y 1+8+0=9 y si la divido en cuatro partes, etc... siempre la suma de las cifras resulta 9. ¡Otra vez la magia del número 9! Pero no hay magia por ningún lado. Hay una explicación perfectamente racional a este hecho. Si tienes cualquier número (te propongo 2635, pero escoge el que tú quieras) y le restas la suma de sus cifras (2+6+3+5=16, 2635-16=2619), lo que te queda es múltiplo de 9; en efecto 2619/9=291, exacto. ¿A qué se debe esto? No entro en muchos detalles, pero mira lo que sigue:
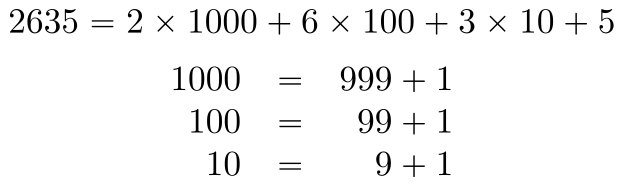
esos unos que quedan a la derecha son los responsables de separar las cifras del número, pero observa que lo que tienen a la izquierda es precisamente un múltiplo de nueve. Entonces, si originalmente el número fuera múltiplo de 9 (como 360) entonces la suma de sus cifras también será múltiplo de 9. No hay ninguna magia: todo lo resuelve el pensamiento racional. A menos que pensemos que disponer de un pensamiento racional es un hecho mágico... discusión cuya profundidad me está vedada.
Pero falta más según el vídeo: la mitad de la circunferencia, su cuarta parte, su octava parte... todas cumplen con que la suma de sus dígitos se reduce a 9. ¡Por supuesto! Después de todo 360=9x40 y las divisiones por 2 afectan al 40 y dejan quieto al 9. De manera que podemos decir, en un sentido bastante extendido para incluir los decimales que nos den, que todos los resultados son múltiplos de 9 y por lo tanto la suma de sus dígitos se reducirá a 9 finalmente.
La magia desaparece cuando nos damos cuenta de que en un sistema de otra base esta propiedad ya no es válida. Por ejemplo, en el sistema octal 360 se escribe 550 (me crees o sacas la cuenta, tú decides, lector). Pero, si te fijas en la tabla de sumar que tienes arriba 5+5+0=12 y 1+2=3. ¡No da 9! Pero ahora te tengo una sorpresa curiosa. Supongamos que en vez de 360, la circunferencia tuviera 280 grados. Este es un número múltiplo de 7 y en el sistema octal se escribe 430. Pero 4+3+0=7. ¡El número mágico ahora es el 7!... En realidad lo que sucede es que si tenemos un sistema de numeración de cualquier base, los números que sean múltiplos del dígito más alto reducirán la suma de sus cifras a ese dígito. No lo voy a demostrar, pero a lo mejor algún curioso lo intenta.
Por cierto, el vídeo dice que todo esto es consecuencia de la teoría de los vórtices. ¡Vaya usted a saber qué es eso! Pero nada mejor que un nombre misterioso para caerle a embustes a la gente.
Nota: Excepto la de los Simpsom, todas las imágenes que aparecen en el post son mías.
Bueno por algo siempre dicen que todos los dias se aprende algo nuevo
Me alegra saberlo, @merryslamb