
Bild Referenz: https://commons.wikimedia.org/wiki/File:Pseudobin%C3%A4rersuchbaumziel.svg
Intro
Hallo, ich bin's @drifter2! Das heutige Thema sind Binäre Suchbäume die am englischen Artikel "C Binary Trees" basiert sind, der von meinen Hauptaccount @drifter1 ist. Da ich dort direkt und nur über solche spezielle Bäume geredet habe, werden wir bei der heutigen Übersetzung erstmals auch über Bäume und Binäre Bäume generell reden. Dadurch werdet ihr besser verstehen wieso wir nur diese eine spezielle Art brauchen. Also dann fangen wir dann mal an!
Baum Datenstruktur generell
Ein Baum ist eine Datenstruktur und ein abstrakter Datentyp. Mit dieser Struktur kann man hierarchische Strukturen abbilden. Ähnlich wie bei Listen nennt man die vorgegebenen Objekte Knoten (Nodes auf Englisch). Meistens speichert man nur die so genannte Wurzel (Root auf Englisch) die uns den Zugriff auf alle anderen, untergeordneten Knoten zulässt. Jede solche Verbindung-Verweis nennt man meistens Kante. Es ist üblich die untergeordneten Knoten als Kinder (Child-nodes auf Englisch) zu bezeichnen und dem verweisenden Knoten als Elternteil (Parent-node auf Englisch). Viel mehr Genealogie Bezeichnungen werden auf verwendet um die "Verwandtschaftsbeziehung" der Knoten zu beschreiben. Knoten ohne Kinder nennt man Blätter (Leafs auf Englisch). Meistens dürfen alle Knoten nur ein Elternteil haben, außer es handelt sich um die Wurzel die natürlich kein Elternteil hat. Die Höhe des Baums kann sehr leicht mit der maximalen Anzahl von Kanten gefunden werden, wenn man von der Wurzel zum entferntesten Blatt geht. Meistens teilt/trennt man den Baum auch in Stufen ein. Jede Stufe enthält die Knoten die die selbe Anzahl an Sprüngen-Kanten von der Wurzel entfernt sind.
All das ist wird sehr schön beim folgenden Baum-Diagramm angezeigt:
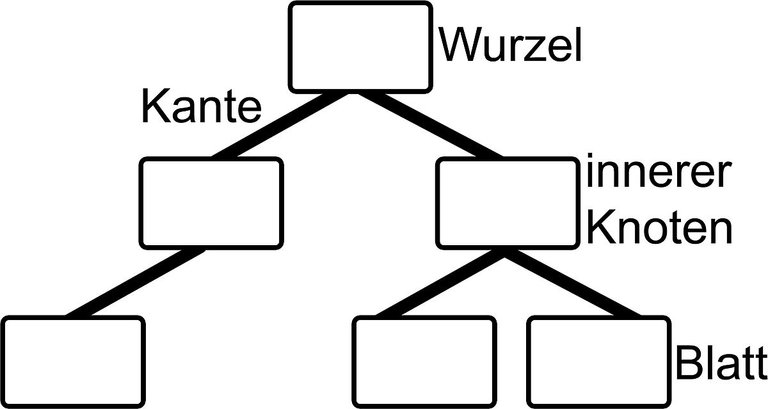
Bild Referenz: https://de.wikipedia.org/wiki/Datei:Bin%C3%A4rBaum_Beschriftung.jpg
Binärer Baum
Jede Knote in einem abstrakten Baum darf unendlich viele Kinder habe. Ein sehr wichtiger Spezialfall ist der so genannte Binärbaum, wo jeder Knoten höchstens zwei Kinder haben darf. Einen solchen Baum kann man sehr leicht mit einer einfach verketteten Liste vergleichen. Jedes Element und jeder Knoten hat nun höchstens zwei Nachfolger, anstatt einen den eine "leichte" Liste zulässt. Wenn einer der Nachfolger nicht existiert nennt man diesen Knoten einen NULL-Knoten. Sind Beide Nachfolger NULL-Knoten dann handelt es sich natürlich von einem Blatt oder Blattknoten.
So ein Baum sieht wie folgend aus:
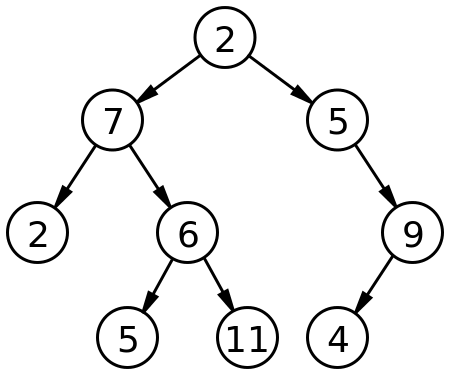
Bild Referenz: https://en.wikipedia.org/wiki/File:Binary_tree.svg
Ein paar wichtige Baumtypen:
- Ein binärer Baum ist vollständig ausgeglichen wenn die maximale und minimale Stufenhöhe (beim linken und rechten Unterbaum) sich nur um eins unterscheiden.
- Ein binärer Baum ist geordnet, wenn die Daten eine Ordnungsrelation erfüllen, was heißt das die Knoten vergleichbar sind und dadurch der linke Nachfolger "kleiner" und der rechte Nachfolger "größer" sind.
Binärer Suchbaum
Eine spezielle Art eines geordneten Binärbaums sind die so genannten Binären Suchbäume (Binary Search Trees - ΒST's). Diese Bäume müssen die folgenden Bedingungen erfüllen:
- Die Elemente erfüllen eine Ordnungsrelation, sind also vergleichbar (geordneter Baum)
- Dadurch enthält der linke Teilbaum eines Knoten immer nur Elemente die kleiner sind als das Knoten-Εlement. Natürlich enthält der rechte Teilbaum des Knotens nur Elemente die größer sind.
- Es gibt keine doppelten Einträge (außer man hat einen zweite, dritte usw. Vergleichs-Bedingung)
- Alle Knoten und Teilbäume müssen all diese Bedingungen erfüllen.
Meistens sprechen wir über eine '<' Ordnungsbedingung bei Zahlen oder Zeichenketten (Strings). Durch eine solche Anordnung wird die Suche eines gewissen Element's natürlich viel effizienter und schneller. Dadurch braucht man natürlich aber auch viel mehr Zeit um einen neuen Wert einfügen zu können, oder sogar einen Wert zu löschen. Diese Operationen sind von einer O(h)-Komplexität, wo h die Höhe (height) des Baums ist. oder die Anzahl an Stufen (Layers). Ein Ganzzahl-Baum sieht wie folgend aus:

Bild Referenz: https://commons.wikimedia.org/wiki/File:Binary_search_tree.svg
Implementation in C-Sprache
Gehen wir jetzt mal in die Implementation dieses letzten Typs ein. Ähnlich wie bei Listen wird eine solche Dynamische Struktur wieder als Struktur (struct) definiert. Jede Knote-Node hat höchstens zwei Nachfolgeknoten, dass heißt das wir zwei Zeiger-Pointer auf solche Baumknoten-Treenodes haben werden, und natürlich auch die eigentlichen Daten des Knoten. Das sieht in Code wie folgend aus:
typedef struct TNode{ // Baumknote // Daten struct TNode *left; // linker Nachfolger struct TNode *right; // rechter Nachfolger}TNode;Die erste Knote oder Wurzel-Root wird natürlich wieder als Zeiger-Pointer abgespeichert, genau wie bei Listen, und wieder auf NULL initialisiert, etwas das uns anzeigt ob der Baum leer ist. Als Code sieht das wie folgend aus:
TNode *root = NULL;Die wichtigsten Operationen die uns an solchen Bäumen interessieren sind:
- Einfügen (insert) eines neuen Elements
- Löschen (delete-remove) eines Elements (das sehr Komplex ist)
- Suche (search) nach einem gewissen Element
- Durchlaufen (Traversal) / Αusdrucken (Printing) eines Baums in 3 wegen: preOrder, inOrder, postOrder
Alle Operationen können leicht als Rekursive Funktionen implementiert werden!
Einfügen
Um eine neue Baum-Knote einfügen zu können muss man erstmal eine neue erstellen, ähnlich wie bei den Listen. Der Code für eine solche neue Knote (new Node - nn) ist:
TNode *nn; nn = (TNode*)malloc(sizeof(TNode)); // fuer alle Daten des Baumknoten nn->val = val; // Zeiger muessen auf NULL initialisiert werden nn->left = NULL; nn->right = NULL;Vor dem Einfügen werden wir immer kontrollieren ob der Baum leer ist. Wenn ja wird die neue Knote natürlich unsere "neue" Wurzel sein. Wenn nicht muss man dann durch den Baum mit einer binären Suche den richtigen Einfüge-Punkt finden, indem man den Wert des zu-einfügenden Knotens mit dem "jetzigen" Knoten vergleicht. Das geht ganz leicht Rekursiv mit dem folgenden Algorithmus:
TNode* insert(TNode *root, int val){ // neuer Knoten TNode *nn; nn = (TNode*)malloc(sizeof(TNode)); nn->val = val; nn->left = NULL; nn->right = NULL; // kontrollieren ob Baum leer ist if(root == NULL){ // nn als neue Wurzel zurueckgeben // oder wegen Rekursion zum richtigen // Punkt einfuegen (als Kind von einem Knoten) return nn; } if(val < root->val){ // Funktion Wiederausfuhr fuer linke Seite root->left = insert(root->left, val); return root; } else if(val > root->val){ // Funktion Wiederausfuhr fuer rechte Seite root->right = insert(root->right, val); return root; }}Wie ihr sehen könnt ist diese komplexe Logik sehr leicht implementierbar durch eine solche Rekursive Vorgehensweise. Eine Iterative Lösung bei einem rekursiven Problem ist sehr schwer zu implementieren.
Löschen
Beim Löschen eines Knotens hat man's aber nicht so leicht! Die Vorgehensweise ist viel komplizierter. Es gibt verschiedene Fälle die man in Anspruch nehmen muss. Unser Algorithmus-Code muss natürlich diese Fälle von einander unterscheiden und erkennen, um die richtigen Schritte-Aufgaben auszuführen.
Gehen wir mal in jeden dieser Fälle ein...
Knoten ist ein Blatt:
Das ist der einfachste Fall. Ein solcher Blattknoten ist ja sozusagen bereits am Ende des Baums und zeigt/verweist deswegen auf keine weiteren Knoten. Das heißt das wir nur das Elternteil dieses Knoten finden müssen und den Zeiger auf den gesuchten Knoten auf NULL setzen müssen.
Knoten hat nur ein Kind:
Wenn ein Knoten nur ein Kind hat, muss mann nur den Elternteil-Zeiger zu dem Kind-Zeiger umtauschen. Dadurch wird der Knoten gelöscht und durch sein (seine - wenn Unterbaum) Kind ersetzt.
Die Zwei ersten Fälle kann man sehr leicht zu einen einzigen Fall zusammenfassen, da beim ersten Fall ja beide Kinder NULL-Knoten sind, das heißt das wir die selbe Operation ausführen.
Knoten hat zwei Kinder:
Der schwerste Fall sind "Zwei Kinder". Hier muss der zu-löschende Knoten durch seinen Nachfolger (successor auf Englisch) ersetzt werden. Natürlich muss dafür sorgen das man nicht zwei dieser Nachfolgerknoten im Baum hat. Doppelte Einträge sind ja verboten.
Also, muss man die folgenden zwei Fälle implementieren:
- Knoten hat keine oder nur ein Kind (wo man auch kontrolliert ob es links oder rechts ist)
- Knoten hat zwei Kinder (das auch die Suche nach einem Nachfolger enthaltet)
Nachfolger (Successor):
Starten wir erstmal mit der Suche nach dem Nachfolger. Als Nachfolger bezeichnen wir den Knoten mit dem nächst höchsten Wert nach dem jetzigen (zu-löschenden) Knoten. Das heißt das wir vom rechten Kind starten und dann das Kind von diesen Knoten das ganz links ist finden müssen. Dadurch haben wir dann den Knoten des Baums gefunden der einen Wert größer als dem vom zu-löschende Knoten hat, der aber der kleinste vom rechten Unterbaum ist. Natürlich kann das rechte Kind auch direkt der Nachfolger sein, wenn dieser keinen linken Unterbaum (oder kein linkes Kind) hat.
Die Funktion die den Nachfolger eines Knoten findet sieht wie folgend aus:
TNode* successor(TNode *node){ TNode *cur; // aktuelle-Knote Zeiger zeigt auf unseren Knoten cur = node; // das meist linke (kleinste) Kind finden while(cur->left != NULL){ // aktuelle-Knote Zeiger zeigt auf linken Nachfolger cur = cur->left; } // kleinste Kind zurueckgeben return cur;}Eigentliche Löschfunktion:
TNode* delete(TNode *node, int val){ // Kontrollieren ob Baum leer ist if(node == NULL){ printf("Not found!\n"); return node; } if(val < node->val){ // Funktion wieder fuer die linke Seite ausfuehren node->left = delete(node->left, val); return node; } else if(val > node->>val){ // Funktion wieder fuer die rechte Seite ausfuehren node->right = delete(node->right, val); return node; } else{ // Wert gefunden (Faelle) // hat linkes und rechtes Kind if(node->left != NULL && node->right != NULL){ // Nachfolger finden TNode *s = successor(node->right); // Wert vom zu-loeschenden Knoten mit dem // Nachfolger-knoten Wert austauschen node->val = s->val; // Nachfolgerknoten Loeschen node->right = delete(node->right, s->val); return node; } // nur linkes Kind else if(node->left != NULL){ // Kind als Knote setzen node = node->left; return node; } // nur rechtes Kind else if(node->right != NULL){ // Kind als Knote setzen node = node->right; return node; } // kein Kind else{ // Knote einfach auf NULL setzen node = NULL; return node; } } }Um Speicher-effizienter zu sein könnte man den Zeiger-Speicher erstmal mit free() "abweisen" und danach auf NULL setzen. Mit NULL verliert man ja die Speicheradresse und verbraucht umsonst Speicher
Suchen
Die Suche nach einem Knoten/Wert ist sehr leicht und ähnlich zu der Einfügen eines neuen Knoten/Werts. Der einzige Unterschied ist das wir jetzt den gefunden Knoten zurückgeben werden als Funktions-Rückgabe, außer der Knoten wurde nicht gefunden, wo wir NULL zurückgeben.
Der Code sieht wie folgend aus:
TNode* search(TNode *root, int val){ // wenn Baum leer ist oder Wert bei der Wurzel ist if(root == NULL || root->val == val){ // Wurzel zurueckgeben return root; } // wenn kleiner else if(val < root->val){ // fuer die linke Seite Funktion ausfuehren return search(root->left, val); } // if greater else if(val > root->val){ // fuer die rechte Seite Funktion ausfuehren return search(root->right, val); }}Durchlaufen / Ausdrucken
Einen Binären Baum kann man in (mindestens) drei Weisen durchlaufen-traversieren.
Diese sind:
- PreOrder - wo man erst das aktuelle Element ausgibt und dann erst den linken und anschließlich rechten Teilbaum
- InOrder - wo man den Baum symmetrisch durchläuft (in natürlicher Ausgabe), dass heißt das man erst den linken Teilbaum, dann das aktuelle Element und zuletzt den rechten Teilbaum ausgibt.
- PostOrder - wo man das aktuelle Element ausgibt, nachdem man den linken und rechten Teilbaum traversiert hat.
Der Präfix (Pre-, In-, Post) vor dem Wort "Order" kann euch dabei helfen diese Weisen von einander zu unterscheiden. Der Präfix zeigt ja die Anordnung/Ausgabe der Wurzel-Knote oder auch generell Elternteil-Knote an.
Diese Weisen kann man sehr leicht als Rekursive Funktionen implementieren.
PreOrder:
void preorder(TNode *root){ if(root == NULL) return; printf("%d ", root->val); if(root->left != NULL)inorder(root->left); if(root->right != NULL)inorder(root->right);}InOrder:
void inorder(TNode *root){ if(root == NULL) return; if(root->left != NULL)inorder(root->left); printf("%d ", root->val); if(root->right != NULL)inorder(root->right);}PostOrder:
void postorder(TNode *root){ if(root == NULL) return; if(root->left != NULL)inorder(root->left); if(root->right != NULL)inorder(root->right); printf("%d ", root->val);}Wie ihr sehen könnt mussten wir nur den Platz der Ausdruckung ändern...
Ein komplettes Beispielprogramm
Zuletzt hier noch ein komplettes Beispiel:
int main(){ // Wurzel auf NULL initialisieren TNode *root = NULL; // Knoten hinzufuegen root = insert(root, 10); root = insert(root, 15); root = insert(root, 5); root = insert(root, 7); root = insert(root, 3); root = insert(root, 13); root = insert(root, 21); // Knoten loeschen root = delete(root, 5); root = delete(root, 10); root = delete(root, 21); // Nach 7 suchen TNode *s; s = search(root, 7); if(s == NULL){ printf("Not found!\n"); } else{ printf("%d was Found!\n", s->val); } // In allen Weisen Durchlaufen/Ausdrucken preorder(root); printf("\n"); inorder(root); printf("\n"); postorder(root); printf("\n");}Referenzen:
- https://de.wikipedia.org/wiki/Baum_(Datenstruktur)
- http://www.straub.as/c-cpp-qt-fltk/c/binary-trees.html
- https://de.wikibooks.org/wiki/Algorithmen_und_Datenstrukturen_in_C/_Bin%C3%A4re_B%C3%A4ume
- http://www.u-helmich.de/inf/BlueJ/kurs121/folge17/folge17-2.html
- https://straub.as/c-cpp-qt-fltk/c/binary-search-tree.html
- https://steemit.com/programming/@drifter1/programming-c-binary-trees
Vorherige Artikel
Grundlagen
Einführung -> Programmiersprachen, die Sprache C, Anfänger Programme
Felder -> Felder, Felder in C, Erweiterung des Anfänger Programms
Zeiger, Zeichenketten und Dateien -> Zeiger, Zeichenketten, Dateiverarbeitung, Beispielprogramm
Dynamische Speicherzuordnung -> Dynamischer Speicher, Speicherzuweisung in C, Beispielprogramm
Strukturen und Switch Case -> Switch Case Anweisung, Strukturen, Beispielprogramm
Funktionen und Variable-Gueltigkeitsbereich -> Funktionen, Variable Gueltigkeitsbereich
Datenstrukturen
Rekursive Algorithmen -> Rekursion, Rekursion in C, Algorithmen Beispiele
Verkettete Listen -> Datenstrukturen generell Verkettete Liste, Implementation in C (mit Operationen/Funktionen), komplettes Beispielprogramm
Schlusswort
Und das war's dann auch schon mit dem heutigen Artikel und ich hoffe ich hab alles verständlich erklärt. Νächstes mal werden wir mit Warteschlangen weiter machen (erstmals implementiert mit Feldern-Arrays).


Keep on drifting! ;)
Hello! Your post has been resteemed and upvoted by @ilovecoding because we love coding! Keep up good work! Consider upvoting this comment to support the @ilovecoding and increase your future rewards! ^_^ Steem On!

Reply !stop to disable the comment. Thanks!
Hi! I am a robot. I just upvoted you! I found similar content that readers might be interested in:
http://www.straub.as/c-cpp-qt-fltk/c/binary-trees.html