Bild Referenz: https://commons.wikimedia.org/wiki/File:Circurlar_linked_list.png
Intro
Hallo, ich bin's @drifter2! Das heutige Thema sind wieder mal Listen und Warteschlangen in die wir dieses mal erweitern um Fortgeschrittenere Datenstrukturen zu erstellen! Dieser Artikel ist an meinen englischen Artikel: "C Advanced Lists and Queues" basiert, von wo ich den Code nehmen werde. Natürlich werde ich nicht nur übersetzen sondern auch ein bisschen Theorie auf anderen Referenzen hinzufügen um alles kompletter zu gestalten. Also dann fangen wir dann mal an!
Doppelt verkettete Listen
Wie bereits im Artikel über "einfach" verkettete Listen erwähnt wurde kann man auch Doppelt und Zirkulär verkettete Listen implementieren. Fangen wir erstmal mit Doppelt verketteten Listen an. Eine solche Liste besteht aus Knoten (Nodes auf Englisch), die jetzt durch zwei Zeiger miteinander verbunden sind, anstatt einen. Das heißt das man einen Zeiger auf den Nachfolger-Knoten (nächster Knoten - next node auf Englisch) und zusätzlich noch einen Zeiger auf den Vorgänger-Knoten (vorheriger Knoten - previous node auf Englisch) hat. Die Funktionen sind analog zu denen einer einfach verketteten Liste. Eine solche Liste ist nützlich bei Problemen wo man leicht nach vorne und nach hinten iterieren muss um schneller und einfacher Elemente an beliebigen Positionen zu löschen oder neue einzufügen.
Die Knote einer solchen Liste kann mit Hilfe der gleichen struct definiert werden die wir auch bei einfach verketteten Listen hatten. Diese war:
typedef struct Node{ int val; struct Node *next;}Node;Wir müssen jetzt nur noch einen zweiten Zeiger hinzufügen der auf den Vorgänger (prev) zeigt. Also, ist die endgültige Knoten-Struktur nun:
typedef struct Node{ int val; struct Node *next; struct Node *prev;}Node;Dieser zweite Zeiger wird und dabei helfen die Löschfunktion zu verkleinern und natürlich ist das Rückwärts-Iterieren der Liste nun nicht mehr ein komplett Rekursives Problem. Alle Funktionen die wir bei einfachen Listen implementiert haben Funktionen schon fast. Wir müssen also nur noch den prev-Zeiger ergänzen.
Ein neuer Knoten wird jetzt mit folgenden Code erschaffen:
Node *nn;nn = (Node*)malloc(sizeof(Node));nn->val = val;nn->next = NULL;nn->prev = NULL; // das einzige neueFangen wir dann mal an mit den Funktionen!
Einfügen (Insert)
Einfügen am Anfang:
Node *insertFirst(Node *head, int val){ Node *nn; // neuen Knoten erstellen nn = (Node*)malloc(sizeof(Node)); nn->val = val; nn->next = NULL; nn->prev = NULL; // Kontrollieren ob Liste leer ist if(head == NULL){ // wenn ja Zeiger zu nn zurueckgeben return nn; } // Kopf der Liste wird nun der neue next-Zeiger von 'nn' nn->next = head; // nn zurueckgeben als Kopf return nn; }Einfügen am Ende:
Node *insertLast(Node *head, int val){ Node *nn, *cur; // neuen Knoten erstellen nn = (Node*)malloc(sizeof(Node)); nn->val = val; nn->next = NULL; // Kontrollieren ob Liste leer ist if(head == NULL){ // wenn ja Zeiger zu nn zurueckgeben return nn; } // Jetzige-Knote Zeiger auf Kopf zeigen lassen cur = head; // Mit While-loop letztes Element finden while(cur->next != NULL){ // cur-Zeiger zeigt auf seinen Nachfolger cur = cur->next; } // Der Nachfolger vom letzten Knoten wird nn cur->next = nn; // Der Vorgaenger von nn ist nun der "vorherige" letzte Knoten nn->prev = cur; // Kopf wieder zurueckgeben return head; }Löschen (Delete)
Löschen am Anfang:
Diese Funktion ändert sich gar nicht!
Hier noch mal der Code:
Node* deleteFirst(Node *head){ // Kontrollieren ob Liste leer ist if(head == NULL){ // Liste ist leer printf("Empty List!"); return head; } // "next"-Zeiger zurueckgeben, also die Liste nach dem Kopf return head->next;}Löschen am Ende:
Das wird nun viel leichter, da wir jetzt direkt zu dem letzten Knoten gehen können und den Nachfolger vom Vorgänger-Knoten auf NULL setzen.
Node* deleteLast(Node *head){ Node *cur; // Kontrollieren ob Liste leer ist if(head == NULL){ // Liste ist leer printf("Empty List!"); return head; } // Kontrollieren ob es sich um das einzige Element handelt if(head->next == NULL){ // Liste wird jetzt NULL return NULL; } // aktuelle-Knote Zeiger zeigt auf Kopf der Liste cur = head; // mit Loop das letzte Element finden while(cur->next != NULL){ // cur-Zeiger zeigt auf das naechste Element cur = cur->next; } // next-Zeiger vom vorherigen (prev) Knoten auf NULL setzen cur->prev->next = NULL; // Listenkopf zurueckgeben return head;}Löschen einer spezifischen Knote:
Diese vorherige Funktion kann sehr leicht erweitert werden um einen spezifischen Knoten zu löschen! Wir müssen ja nur den eigentlichen Knoten den wir suchen finden und dann den Nachfolger seines Vorgängers zu dem Nachfolger des gesuchten Knoten setzen (das auch NULL sein kann). Das alles sieht in Code wie folgend aus:
Node* deleteVal(Node *head, int val){ Node *cur; int found = 0; // Kontrollieren ob Liste leer ist if(head == NULL){ // Liste ist leer printf("Empty List!"); return head; } // Kontrollieren ob es sich um das einzige Element handelt if(head->next == NULL){ // Wert vergleichen if(head->val == val){ return NULL; } printf("%d was not found!\n", val); return head; } // aktuelle-Knote Zeiger zeigt auf Kopf der Liste cur = head; // Mit Loop nach dem Element suchen while(cur->next != NULL){ // Wert vergleichen if(cur->val == val){ found = 1; // gefunden break; } // cur-Zeiger zeigt auf das naechste Element cur = cur->next; } // Kontrollieren ob gefunden wurde if(found == 0){ printf("%d was not found!\n", val); return head; } // next-Zeiger vom Vorgaenger (prev) Knoten // zu Nachfolger (next) des gefundenen Knoten setzen cur->prev->next = cur->next; // Listenkopf zurueckgeben return head;}
Die Suche nach einem Element und das durch-iterieren und ausdrucken der Listen-Elemente kann wieder mit genau den gleichen Funktionen gemacht werden (wie ihr vielleicht bereits bemerkt habt, da diese letzte Löschfunktion eine Suche enthielte). Natürlich könnt ihr beim Ruckwärts-iterieren auch zum Letzten Knoten gehen und dann durch seine Vorgänger zurückgehen.
Zirkuläre Listen
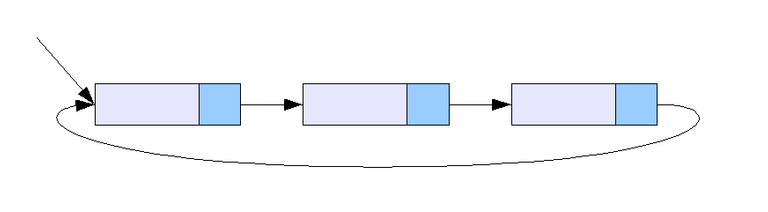
Eine so genannte Zirkuläre Liste kann sehr leicht implementiert werden durch die Erweiterung der normalen oder auch doppelt verketten Liste. Das Letzte Element muss einfach auf das Erste zeigen, so dass wir diese zirkulär durch-iterieren können. Damit wird natürlich das Einfügen und Löschen eines Elements am Ende der Liste viel schneller. Das Problem hierbei ist aber das wir nun aufpassen müssen das es eine Abbruchbedingung gibt so dass wir keine Endlosschleife erschaffen. Das beste hier ist den Kopf irgendwie zu markieren so dass man weiß wann man einen kompletten Durchlauf gemacht hat.
Ich lasse mal Code und so aus damit ihr selber experimentieren könnt! :)
Vorrangwarteschlange (oder Prioritätsschlange)
Eine Vorrangwarteschlange (Priority Queue auf Englisch) ist eine spezielle, erweiterte Form einer Warteschlange. Bei dieser Datenstruktur werden die Element nach einer gewissen Reihenfolge/Priorität eingefügt. Die Priorität eines Element wir durch einen Schlüssel festgelegt. Man kann natürlich diese Priorität mit vielen verschiedenen Weisen implementieren.
Ein einfacher Weg um die Warteschlange die wir bereits implementiert haben zu erweitern ist die Erweiterung der Knoten-Element-Struktur, so dass diese eine Priorität (oder Schlüssel) Variable enthält. Das Element mit der höchsten Priorität muss ja als erstes entfernt werden. Da wir ja immer nur aus dem Anfang (front) der Warteschlange Elemente rausnehmen können werden wir beim Einfügen eines Elements dafür sorgen das dieses bei der richtigen sortierten Stelle eingefügt wird.
Als Struktur sieht eine solche Prioritätsschlange wie folgend aus:
typedef struct Node{ int val; int priority; struct Node *next;}Node;typedef struct Queue{ Node *front; Node *rear;}Queue;Löschen (Dequeue) und Ausdrucken (Print):
Die Lösch- und Ausdruck-Funktionen die wir bei Warteschlangen implementiert haben, bleiben genau gleich, da wir ja immer noch vom Front-Index löschen und die Priorität bereits von der Einfüge-Funktion erledigt wird.
int dequeue(Queue *Q){ int val; // Kontrollieren ob Warteschlange leer ist if(Q->front == NULL){ return -1; } // Wert von Front abspeichern val = Q->front->val; // Kontrollieren ob es sich um das einzige Element handelt if(Q->front == Q->rear){ Q->front = Q->rear = NULL; } // Einfachster Fall else{ // Front-Zeiger zeigt nun auf seinen Nachfolger Q->front = Q->front->>next; } // Wert zurueckgeben return val; }void print(Queue Q){ int val; // Kontrollieren ob Warteschlange leer ist if(Q.front == NULL){ printf("Queue is Empty!\n"); return; } // dequeue() ausfuehren solange es Elemente gibt while((val= dequeue(&Q)) != -1){ printf("%d ", val); } printf("\n");}Einfügen(Enqueue):
Nun zum eigentlichen neuen! Die Einfüge-Funktion muss ja die richtige Stelle finden so das die Liste nach Priorität sortiert ist. Das muss nach jeder Einfügung bestehen. Wir könnten direkt durch-iterieren und die richtige Stelle finden, durch die Hilfe des Nachfolgers. Der Nachfolger ist hier aber nicht leicht erreichbar wie bei Doppelt verketteten Listen und wir wollen die Schlange nicht doppelt-verlinkt implementieren! Anstatt das wir wieder mal nach dem vorherigen Knoten suchen, etwas das aber schneller ist, werden wir das neue Element einfach am Anfang der Liste einfügen und dann die Warteschlange sortieren. Die Sortierung ist natürlich viel leichter, wird aber natürlich Zeit kosten!
void enqueue(Queue *Q, int val, int priority){ Node *cur, *nn, temp; // neuen Knoten erstellen nn = (Node*)malloc(sizeof(Node)); nn->val = val; nn->priority = priority; nn->next = NULL; // Kontrollieren ob Warteschlange leer ist if(Q->front == NULL){ Q->front = Q->rear = nn; return; } // Neue Knote am Anfang einfuegen nn->next = Q->front; Q->front = nn; // Sortieren mit Hilfe der Prioritaet cur = Q->front; while(cur->next != NULL){ // priority-Wert vergleichen if(cur->priority < cur->next->priority){ // anstatt das wir die Knoten selber tauschen // werden wir die Knotenwerte austauschen // mit Hilfe eines temporaeren Knotens temp = *cur; cur->val = cur->next->val; cur->priority = cur->next->priority; cur->next->val = temp.val; cur->next->priority = temp.priority; } cur = cur->next; }}Komplettes Programm:
int main(){ // Warteschlange initialisieren Queue Q; Q.front = Q.rear = NULL; print(Q); // 5 einfuegen mit priority 2 enqueue(&Q, 5, 2); print(Q); // 10 einfuegen mit priority 5 enqueue(&Q, 10, 5); print(Q); // 3 einfuegen mit priority 1 enqueue(&Q, 3, 1); print(Q); // Elemente rausnehmen int val; val = dequeue(&Q); if(val == -1){ printf("Queue is Empty!\n"); } else{ printf("%d\n", val); } print(Q); }Da 10 die höchste Priorität hat, wird 10 weggenommen und nicht der erste Wert (5) oder letzte Wert (3), da ja 3 direkt zum Ende sortiert wird und 5 eine kleinere Priorität als 10 hat und die Werte ausgetauscht wurden.
Referenzen:
- http://www.straub.as/c-cpp-qt-fltk/c/double-linked-list.html
- https://perlgeek.de/de/artikel/doppelt-verkettete-listen
- https://de.wikipedia.org/wiki/Vorrangwarteschlange
- https://steemit.com/programming/@drifter1/programming-c-advanced-lists-and-queues
Vorherige Artikel
Grundlagen
Einführung -> Programmiersprachen, die Sprache C, Anfänger Programme
Felder -> Felder, Felder in C, Erweiterung des Anfänger Programms
Zeiger, Zeichenketten und Dateien -> Zeiger, Zeichenketten, Dateiverarbeitung, Beispielprogramm
Dynamische Speicherzuordnung -> Dynamischer Speicher, Speicherzuweisung in C, Beispielprogramm
Strukturen und Switch Case -> Switch Case Anweisung, Strukturen, Beispielprogramm
Funktionen und Variable-Gueltigkeitsbereich -> Funktionen, Variable Gueltigkeitsbereich
Datenstrukturen
Rekursive Algorithmen -> Rekursion, Rekursion in C, Algorithmen Beispiele
Verkettete Listen -> Datenstrukturen generell Verkettete Liste, Implementation in C (mit Operationen/Funktionen), komplettes Beispielprogramm
Binäre Suchbäume -> Baum Datenstruktur generell, Binärer Baum, Binärer Suchbaum, Implementation in C-Sprache (mit Operationen/Funktionen), komplettes Beispielprogramm
Warteschlangen implementiert mit Feldern -> Warteschlange als Datenstruktur, Implementation einer Warteschlange mit Feldern in C-Sprache, komplettes Beispielprogramm
Stapel implementiert mit Feldern -> Stapel als Datenstruktur, Implementation eines Stapels mit Feldern in C-Sprache, komplettes Beispielprogramm
Warteschlangen und Stapel implementiert mit Verketteten Listen -> Liste, Warteschlange und Stapel mit Liste implementieren in C-Sprache.
Schlusswort
Und das war's dann auch schon mit dem heutigen Artikel und ich hoffe euch hat dieser Artikel gefallen. Νächstes mal werden wir über fortgeschrittene Bäume reden!


Keep on drifting! ;)
Hello! Your post has been resteemed and upvoted by @ilovecoding because we love coding! Keep up good work! Consider upvoting this comment to support the @ilovecoding and increase your future rewards! ^_^ Steem On!

Reply !stop to disable the comment. Thanks!
Guten Tag,
Ich bin der Germanbot und du hast von mir ein Upvote erhalten! Als Upvote-Bot möchte ich, hochwertigen deutschen Content fördern. Noch bin ich ein kleiner Bot, aber ich werde wachsen.
Jeden Tag erscheint ein Voting Report, in dem dein Beitrag mit aufgelistet wird. Auch werden meine Unterstützer mit erwähnt. Mach weiter so, denn ich schaue öfter bei dir vorbei.
Gruß
GermanBot
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!