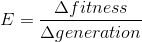
Abstract
This essay studies how effective a chosen group of different types of genetic algorithms are at finding the shortest path between two points. As finding the shortest path between two lines is a very simple optimization problem, the significance of this investigation lies in the convention of using genetic algorithms to solve very complicated problems. This, in my opinion, neglects the potential of this type of problem solving at lower levels of complexity.
So, a more detailed version of the essay is: “Analysis of the effectiveness of different types of genetic algorithms in terms of a simple optimization problem”.
The first section of the essay provides background information in order to allow the reader to understand the way I have approached this investigation. Along with some brief historical background, I give a summary of what a genetic algorithm is, what different types there are, and which types are used for data collection. Data was gathered through a program I wrote with the Java programming language for this particular investigation. The data is specifically generated in terms of finding the shortest path between two points. However, the data is analyzed in consideration of how well it would fare for the solution of any simple optimization problem.
The last part of the essay provides the conclusion, which states that the type of genetic algorithm which is most effective at finding the shortest path between two points uses Linear Rank selection and arithmetic reproduction. The conclusion also states that a genetic algorithm using Roulette ranked selection and arithmetic reproduction would be similarly effective at solving simple optimization problems in general. Lastly, the evaluation expresses the limitations to the research, and how it could be improved.
1. Introduction
With the conceptualization of evolutionary programming in 1954 by Nils Aall Baricelli, and the development of genetic algorithms by professor John Holland during the 1960’s and 1970’s, a new door to computing was opened. By realizing that optimization problems could be approached with a method based on natural selection, algorithms could finally take the next step.
Genetic algorithms have several properties as an optimization mechanism. Firstly, they can be used to solve complex problems, such as optimal jet turbine designs. Secondly, they can solve problems with a very large search space, as they do not try every option in the search space. Thirdly, they can be used for problems of which not much is known; no information about how to solve the problem is needed - only what the problem is. However, genetic algorithms do have their drawbacks. They can take a long time to compute, and they will never give an absolutely perfect solution. Also, the transfer of theoretical results to practical success can be challenging, as the simulation of the problem may not be accurate enough for the real life situation.
Although not every type of genetic algorithm will be investigated, due to the vast number of methods, it is the aim of this investigation to cover the main principles of the different methods, how effective they are, and why they act the way they do.
The reason the efficiency of certain genetic algorithms in terms of a simple optimization problem is being researched, is because genetic algorithms are usually only applied to very complex problems. Although genetic algorithms are often seen as very complex, in truth they are not. They are simple algorithms based on the principle of natural selection. Therefore, this paper serves to show that genetic algorithms can be effectively used to find answers to simple optimization problems. Hence, this is an analysis of the effectiveness of different types of genetic algorithms in terms of a simple optimization problem.
2. Genetic Algorithms
2.1 Definition
Genetic algorithms are types of algorithms which take ideas from selective reproduction, such as natural selection or artificial selection. This means that it optimizes data through evaluation, selection and reproduction or mutation
First a random pool of data is created; the population. Each collection or array of data, also referred to as a gene, is then evaluated in terms of the extent to which the gene solves the problem. A selection algorithm is then used to select the ‘fittest’, or most effective, genes from the population. The fittest genes are then either mutated, meaning that the gene’s data is changed, or crossed in order to create a new population of genes. Because only the fittest genes of each population are selected to create the new population, each new population should have fitter genes than its predecessor.
In pseudo code, a genetic algorithm can be represented as:
- choose/generate population
- start loop
- evaluate fitness of each gene
- select parent genes
- mutate or reproduce parent genes
- check for termination
- restart loop
2.2 Selection Algorithms
Selection algorithms are designed to select parent genes from the population.
Roulette wheel selection
Roulette wheel selection gives each gene the opportunity to be selected as parent in proportion to its fitness. There are different ways to implement this idea in a genetic algorithm. A common method is to take the sum of the fitness of the whole population, generate a random number between zero and the fitness sum, then select the first gene whose fitness is greater than or equal to the random number.
Linear rank selection
This type of selection chooses is the most basic choosing method. Rank selection chooses the parent genes through a fixed percentile. For example, the top 10% of genes could be chosen to create the next generation. Simply put, Rank selection chooses the genes with the best fitness in the population.
Roulette ranked selection
This type of selection initially selects genes through roulette wheel selection, and then selects the best genes through linear rank selection. This selection technique is only a combination of the previous techniques. The reason it was chosen for this investigation is because its results may emphasize aspects of the other two algorithms.
2.3 Mutation Algorithms
Mutation algorithms take one parents gene, mutate its contained information, and create a child gene. Different mutation algorithms vary in the way they mutate the parent gene.
Binary Mutation
Although Binary Mutation is a general terms for several different types of binary mutation, the method discussed here is specifically called bit inversion. As the name suggest, it mutates genes by inverting every bit in the gene.
| - | Binary | Decimal |
|---|---|---|
| Before mutation | 10110011 | 01001100 |
| After mutation | 179 | 76 |
As can be seen, one bit inversion changed the value by 103. One notable aspect of this type of inversion is that the change between the values of genes between generations is not constant.
Arithmetic Mutation
This type of mutation takes the decimal value of a gene and changes it by a random value between a constant range. For example, the arithmetic mutation could change each gene by a Double value between -2 and 2. As this range could definitely be an aspect which could affect the efficiency of the algorithm, this value will be investigated later.
2.4 Reproduction algorithms
Reproduction algorithms take two parent genes, combine the contained information, and create child genes. Reproduction algorithms vary in the way they combine the parent genes, and how many children genes they create.
Arithmetic cross
Reproduction algorithms take two parent genes, combine the contained information, and create child genes. Reproduction algorithms vary in the way they combine the parent genes, and how many children genes they create.
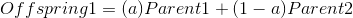
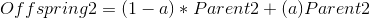
Binary cross
Binary cross, as the name suggests, involves the crossing of the binary values of two genes. There are several different types of binary cross. They involve the combination of both parent’s binary integers around a randomly specified point.
Examples of these are:
One point
The parent genes are combined by first determining a random point and then combining the genes by taking one side of one parent gene and another side from the other parent gene.
| Gene | Binary | Decimal |
|---|---|---|
| Parent 1 | 10110100 | 180 |
| Parent 2 | 01001011 | 75 |
| Offspring | 10110011 | 179 |
Two Point
Uses the same principle as one point binary cross, just that it uses two randomly selected point instead of one.
| Gene | Binary | Decimal |
|---|---|---|
| Parent 1 | 10110100 | 180 |
| Parent 2 | 01001011 | 75 |
| Offspring | 10001100 | 140 |
N Point
Uses the same principle as one point binary cross, just that it uses n randomly selected points, where n is the number of binary integers in the parent genes. What this implies, is that the parent genes are crossed by alternating the parent from which the next binary integer is taken for the offspring.
| Gene | Binary | Decimal |
|---|---|---|
| Parent 1 | 10110100 | 180 |
| Parent 2 | 01001011 | 75 |
| Offspring | 11100001 | 22 |
2.5 Specifics
Termination
An important aspect of genetic algorithms is when it should stop. Due to the random attributes of genetic algorithms, the genes, no matter how long the process has been running, are not likely to be perfect. This implies that termination should take place when the result is optimized to a point of satisfaction. Additionally, the question of whether the termination should be based off the fittest gene of the population or the average of the population also comes into place.
To avoid the issue of knowing when to terminate the process, a slightly different approach will be used to evaluate the different algorithms. Instead of setting a fixed termination point, the rate of evolution of the population will be measured. The way this will be done is discussed in section 6.1.
Replacement
Genetic algorithms also differ in the way new child genes are added to the population. In general, there are two different types of replacement: generational and steady state.
Generational replacement makes each new generation entirely replace the previous population after one loop of the algorithm.
Steady state replacement on the other hand only replaces part of the population after one loop of the algorithm.
Here are some different steady state replacement schemes:
- Replacing worst genes
- Replacing best genes
- Replacing parent genes
- Replacing random genes
- Replacing most similar genes
This investigation, for the sake of simplicity, will only use generational genetic algorithms. In addition, generational algorithms will make changes between generations more apparent, which will help determine the attributes of each different algorithm more clearly.
3. Optimization problem
3.1 Description
In order to be able to determine how effective each type of genetic algorithm is, they all have to be tested with the same optimization problem. This optimization problem is often called the fitness function, as it is an algorithm and therefore a function which determines how fit a gene is.
The simple optimization problem used for this paper is the question of finding the shortest path between two points.
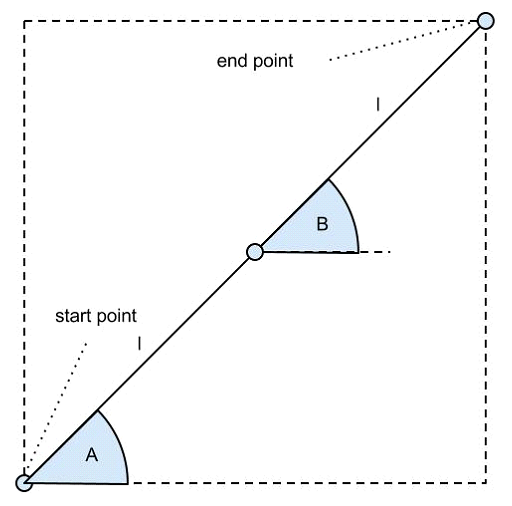
As seen in the diagram above, there are two lines of fixed length l. The end of the first line is attached to the beginning of the second line. The closer the end of the second line is to the end point, the more successfully the problem has been solved.
Only two parameters are going to be inputted into the problem, angle A and B. This means that each gene will only include two pieces of data, more specifically two numbers. The second line is always attached to the first line, and each line’s angle is measured from the horizontal.
Knowing this, two facts about the optimal solution are already known:
- Due to the fixed lengths of both lines, Angles A and B must be equal in order to make the second line touch the end point.
- Angles A and B must both be equal to the optimal angle in order to achieve the shortest path.
3.2 Solving method
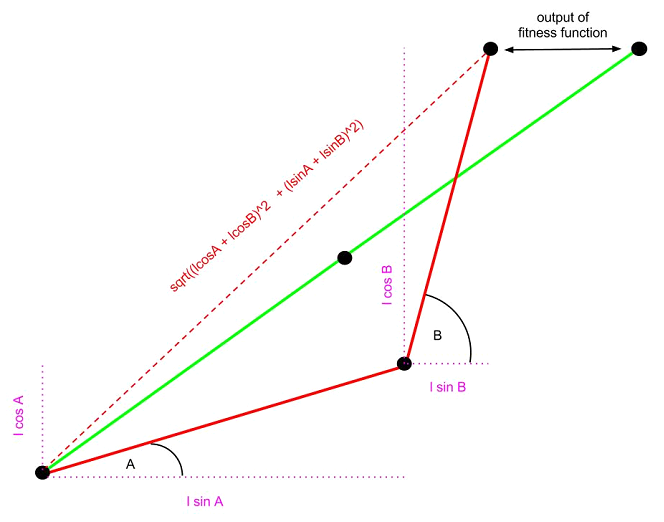
The fact that the angle to the horizontal of each line is known and the lengths of both lines are known allows us to determine each line’s horizontal and vertical components (as seen in the diagram above as the purple dashed line). These calculations are indicated above in purple.
Taking these components and applying them to Pythagoras’ theorem we can find the vector which stretches from the start of the first line to the end of the second line. This vector will be called the resultant line (resLine).
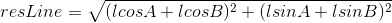
Using the cosine role from here, the distance between the end of the resLine and the end point can be found.
In order to use the cosine rule though, the angle between the optimal line (green line) and the resLine has to be found. Subtracting the average of angles A and B by the optimal angle gives us this angle as it results in the angular distance between both lines. However, if the optimal angle is smaller than the average of angles A and B, the resultant angle would be negative. To avoid this problem, we simply find the modulus of the result:
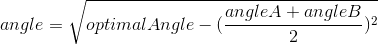
Now that this is known, the cosine rule can be applied:
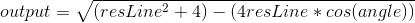
Note that the smaller the fitness, the fitter the gene is, as a shorter distance between the end of the resLine and the end point indicates a fitter gene.
Here are some examples of some genes and their fitness with 45º as the optimal angle:
| Gene | Gene | Fitness |
|---|---|---|
| Angle A | Angle B | - |
| 45.0 | 45.0 | 0 |
| 45.0 | 25.0 | 0.347 |
| 19.24 | 80.23 | 0.316 |
| 0.0 | 0.0 | 1.531 |
4. Method
It may be worthwhile to note that the programming language I used is Java. However, a brief description of the experimental process can be outlined here.
In principle, all data was generated through the application of the following algorithm:
Name: generation
Paramteres: int gen, int selectType, int changeType
Return: array of doubles
Description: This algorithm calculates the average fitness and the average angle of the population after certain number (specified by int gen) of generations. The type of selection and mutation/reproduction algorithm used is specified by the selectType and changeType integer parameters. The average fitness is returned in the first slot of the double array, and the average angle in the second.
Short term results were acquired with the public void earlyPreciseCheck() method in the Driver class. This method calculates the generation() values from 0 to 20 for each possible selection, reproduction and mutation combination. All results are printed into a text file with the name “earlyResults.txt” in the directory of the program.
Long term results were acquired with the public void experiment() method in the Driver class. This method calculates the generation() values from 10^0 to 10^4 generations, in steps of increasing order of magnitude. More specifically, it calculates the generation() values of each possible selection, reproduction and mutation combination, at 10^0, 10^1, 10^2, 10^3 and 10^4 generations. All results were printed into a text file with the name “results.txt” in the directory of the program. Screenshots of these files are included in the appendix.
5. Results
You can find the results here. They would take up too much space on this page.
There is a little problem though...
I wrote this as an innocent 17 year-old, so although I still have 3-4 different versions of the program and the output files, they aren't entirely complete.
I uploaded what I have anyway and as it's an html file so I can upload whatever else I find as I dig deeper.
I also used to have pages of graphs to represent the data, but the descriptions, tables, and scraps of raw data will have to do now.
Thanks for your consideration!
edit:
Thanks for you support!
I uploaded the scraps of code that I found so far. They're in the link above. To be honest, the code is far more substantial than what I have of the results, so if anyone feels like generating more data let me know!
6. Analysis
6.1 Effectiveness
An index of the average rate of change of the average fitness will be used in order to numerically compare the efficiency between the different algorithms. Let the symbol for this index be E (for effectiveness).
The formula used is:
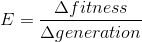
This formula can be used to roughly analyze smaller or larger portions of data. For example, a value for the average rate of change of average fitness for a specific selection, mutation or reproduction algorithm can be used for a range of thousands or generations, dozens of generations or even one generation. This gives the possibility of determining the long term effectiveness or the short term effectiveness.
This can be a powerful tool to analyze different portions of data, as the rate of change of the average fitness is not steady for any of the data collected.
Here are the results for the effectiveness of all the selection, mutation and reproduction algorithm combinations over the 19 generated generations shown in the tables above.
| Algorithm combination | Average rate of change of average fitness over 19 generations |
|---|---|
| Roulette + arithmetic mutation | 0.021979 |
| Roulette + binary mutation | 0.024789 |
| Roulette + binary cross | 0.019684 |
| Roulette + arithmetic cross | 0.020526 |
| Linear Rank + arithmetic mutation | 0.026037 |
| Linear Rank + binary mutation | 0.029547 |
| Linear Rank + binary cross | 0.029906 |
| Linear Rank + arithmetic cross | 0.029721 |
| Roulette ranked + arithmetic mutation | 0.03101 |
| Roulette ranked + binary mutation | 0.029423 |
| Roulette ranked + binary cross | 0.025016 |
| Roulette ranked + arithmetic cross | 0.027645 |
6.2 Analysis of selection algorithms
Roulette Wheel Selection
Short term
The roulette wheel selection method makes the average fitness of each generation’s population decrease at a moderate level. The effectiveness between data points fluctuates over time. This can be seen in combination with all four used mutation and reproduction algorithms. Considering that Roulette Wheel selection shows this, suggests that the generation of a new random population for each data point influences roulette wheel selection more heavily.
Long term
The long term results mainly reveal that the fitness results of the roulette wheel selection do not fluctuate as much over a large number of generations. However, just as in the short term results, roulette wheel selection does not reach fitness values as low as the algorithms including linear rank selection do.
Linear Rank Selection
Short term
Linear rank shows a very strong and steady average effectiveness. Unlike roulette wheel selection, population fitness averages do not change drastically from one generation to another. With all four mutation and reproduction algorithms the effectiveness decreases over time. Once the population’s fitness reaches a level close to its optimum, linear rank selection seems to remain around these values.
Long term
In this case, the long term results emphasize the individual properties of the mutation and reproduction algorithms. All mutation and reproduction methods which include the use of random numbers show clear fluctuations. Arithmetic cross, the only one of these four methods which does not include randomization is given emphasis on its stability and ability to produce very strong fitness values.
Roulette ranked Selection
Short term
The Roulette ranked selection values show strong similarities with the linear rank selection. This is mainly due to the fact that Roulette ranked selection first selects the population through roulette wheel, and makes a selection with linear rank selection. The fact that linear rank selection is used last before the final data of each population’s fitness average indicates why Roulette ranked selection is so similar to linear rank selection.
Long term
These results are very similar to the long term results of the linear rank selection. All reproduction and mutation methods which include randomization have quite strong fluctuations over the long term. Arithmetic cross, however, yields very strong fitness values with no apparent fluctuation in fitness.
6.3 Analysis of mutation algorithms
Binary mutation
Its average effectiveness is the highest out of all four algorithms in the range of generations used to acquire this data. Binary mutation seems to give the best results out of all four algorithms over the short run. The occasional jumps are most likely due to the large changes in values after one mutation as was mentioned in the initial description of the algorithm.
Arithmetic mutation
Arithmetic mutation has the second highest average effectiveness. Unlike the binary inversion, its values between generations do not vary drastically, although they do vary some. This is become the arithmetic mutation can be either positive or negative, meaning that approximately half the time the mutation will be away from the optimum. Over a short range of generations arithmetic mutation seems to be a fairly reliable method of mutation.
Analysis of reproduction algorithms
Binary Cross
Binary Cross has the second lowest average effectiveness out of all mutation and reproduction algorithms. Although the name suggests that the parent angles would converge by crossing them, this is not necessarily true. Due to the method of binary cross used in this investigation, completely different decimal values of angles can be obtained after crossing two angles. This puts binary cross into a similar situation as binary mutation, as its values can change drastically between generations. This method of crossing would probably not fare very well in a long term scenario.
Arithmetic Cross
Arithmetic cross has the lowest average effectiveness out of all mutation and crossing algorithms. Although this seems to be the case, its true strength lies in the stability of its children’s convergence towards the optimum. As seen in the data above, its population’s trend toward the optimum is not interrupted by sudden leaps of fitness or angle values. As seen in the long term results, this reproduction method fares better when run over a large range of generations.
7. Conclusion
It is hard to really determine which algorithm is the best algorithm for solving a simple optimization problem. The different attributes of all the algorithms are all suited for different tasks. This means that the person who is planning to use a genetic algorithm to solve a problem will have to make an analysis of the problem before implementing the code. Like this, the genetic algorithm can be used most efficiently.
It is possible to derive general conclusions from the information gathered. Considering that the investigation explored each type of algorithm with the optimal solution already in mind, both a short and long range in generations were appropriate to investigate the algorithms properties. However, if the optimal solution is not known, a larger range in generation will yield more accurate results. This only works with combinations which yield a stable progression of results though, as an unstable combination, such as linear rank with binary mutation, has a higher chance of going against the optimum over a large range of generations. Therefore, any of the combinations with relatively high effectiveness values, high stability, and strong maximum fitness values should be suited to solve simple optimization problems.
These include,
- Linear rank + Arithmetic cross
- Roulette ranked + Arithmetic cross
However, for this particular problem – finding the shortest path between two lines – an answer can be given.
Out of all combinations of selection and reproduction/mutation algorithms, Linear Rank selection with Arithmetic Cross returns the strongest fitness: 1.89*10^-4. In addition, as can be seen in the table of long term results, this combination is also the most stable, being the only one which does not cause the fitness to change its order of magnitude once reaching 10^-4. Its long term effectiveness, although very high, is not the highest out of all combinations. This is clearly because the long term effectiveness is measured from the 1st generation to the 10000th generation, causing the calculation to omit the effectiveness between generation 0 and 1, which in the case of this combination is higher than any other combination.
8. Evaluation
In general, there are three main limitations regarding the reliability of this investigation. Firstly, due to time acting as a limiting factor, not every different type of genetic algorithm could be investigated. Although the three selection, two reproduction and two mutation methods used give an idea of different types of genetic algorithms, there is no justification behind the selection of these specific methods. A more complete investigation should include a wider range of algorithms. Secondly, constants involved in these methods, such as the range of random deviation in arithmetic mutation were chosen without justification. This was done because of the cost in time for investigating each of these factors did not seem to be worth the benefit. However a more complete paper should include such analyses. Lastly, the optimization problem used raises some issues. Although finding the shortest path between two lines is a simple optimization problem, several different optimization problems would yield an analysis with increased accuracy.
There are also other, possibly less important aspects, which affect the reliability of this investigation. An extension in the amount of data used for the long term results would definitely increase the accuracy of the analysis. This could be done by writing a more efficient data collection algorithm. That only generational algorithms were used also presents a limitation, and could be improved by also applying all selection, mutation and reproduction algorithms to a steady-state approach. For the use of binary cross and mutation, the program includes decimal-integer conversions. However, binary to decimal conversions when working with decimal points always yield truncation errors. These errors are usually very small, but may have still influenced the generated data. Although truncation errors cannot be avoided, it should be clear to the reader that these uncertainties are present.
Finally, the choice of generating a new population for the calculation of each generation’s average fitness and angle also raises some issues. In one sense it decreases the influence the original population has on all other generation’s results. However, it ignores a whole different aspect of the investigation, and therefore should be included for a more complete investigation.
Sources
- Sivaraj, R. "A REVIEW OF SELECTION METHODS IN GENETIC ALGORITHM."International Journal of Engineering Science and Technology (IJEST) 3 (2011): 3793-794. Web. 1 Dec. 2012.
- Obitko, Marek. "XI. Crossover and Mutation." Crossover and Mutation. N.p., 1998. Web. 28 Nov. 2012.
- "Genetic Algorithms: Crossover." Genetic Algorithms: Crossover. NeuroDimension, 2012. Web. 1 Dec. 2012. http://www.nd.com/products/genetic/crossover.htm.
- Noever, David, and Subbiah Baskaran. "Steady-state vs. Generational Genetic Algorithms: A Comparison of Time Complexity and Convergence Properties." (n.d.): n. pag. Web.
- Xifeng, Juan. "Pseudo Code of Genetic Algorithm and Multi-Start Strategy Based Simulated Annealing Algorithm for Large Scale Next Release Problem." N.p., n.d. Web.
- Yaeger, Larry. "Intro to Genetic Algorithms." Lecture. Informatics Indiana. Web. 11 Aug. 2012. http://informatics.indiana.edu/larryy/al4ai/lectures/03.IntroToGAs.pdf.
- Giannakoglou, K. C. "A Design Method For Turbine Blades Using Genetic Algorithms On Parallel Computers." ECCOMAS (1998): n. pag. Ohn Wiley & Sons, Ltd. Web. 24 Aug. 2012. http://velos0.ltt.mech.ntua.gr/research/pdfs/3_041.pdf
Equations and graphs generated w/ Google drive and LateX
other: Portfolio page
steemit: @martin-stuessy
yes
I linked the relevant files in the results section! Let me know if you have any questions and thanks for the support!