Flow.
¿Quién no ha jugado Flow al menos una vez? ¿Quién no ha matado el tiempo en una situación fastidiosa conectando puntos de colores con líneas? No lo sé. Ciertamente, yo si he lanzado mis buenas horas en este simple juego.

Pero que sea simple no significa que sea sencillo (solo pregúntale a un jugador de Sudoku). Yo en mi ociosidad, pensé un día en cómo podría escribir un algoritmo que resolviera un puzzle de Flow arbitrario. Para hacer el cuento corto: nunca lo hice, pero sí logré algo bastante divertido igualmente :) un generador de niveles de Flow.
Sí, como lo oyes. Un pequeño programilla de Python 3 que genera puzzles de Flow del tamaño que quieras. En este post les explicaré cómo funciona, y cómo ustedes pueden hacerlo también; honestamente, es tan sencillo que cualquier persona medianamente acostumbrada a Python podría hacerlo desde cero. Aquí va
El Algoritmo
La forma en que funciona es muy sencilla. Piensa en lo siguiente: lo que hace al juego de Flow complicado es que debes unir los puntos con líneas ininterrumpidas. Es decir, sin pasar una por encima de otra. Cuando tienes cuatro colores es sencillo. Cuando tienes doce colores, no tanto. Pero esto te da una pequeña pista sobre cómo generarlos.
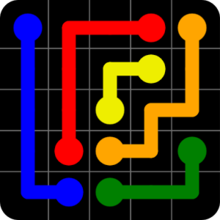
Imagina que tienes un puzzle de 5x5, con cinco colores. En total, han de haber cinco lineas conectando los 10 puntos a pares, según el color. Ahora imagina que tomases esas lineas y las movieras/estiraras para que estuviesen completamente rectas sobre la retícula, así
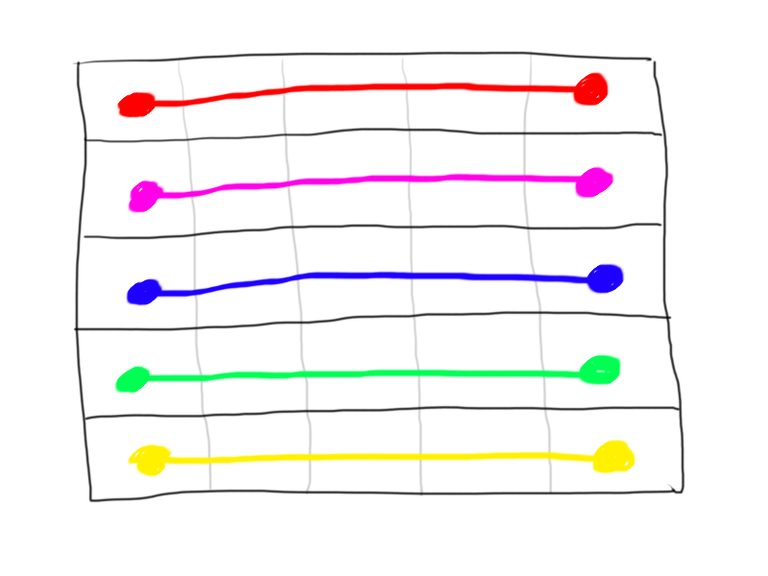
Ciertamente, debe haber alguna manera de pasar de esta configuración al puzzle original. Pero, ¿cómo? Hagámoslo paso a paso; literalmente, un cuadro de retícula a la vez.
Las únicas dos restricciones sobre el puzzle son que
- Ninguna linea debe cruzar a otra
- No deben haber espacios vacíos
En términos más simples, si etiquetamos las partes de la línea como “Extremo y Barriga”
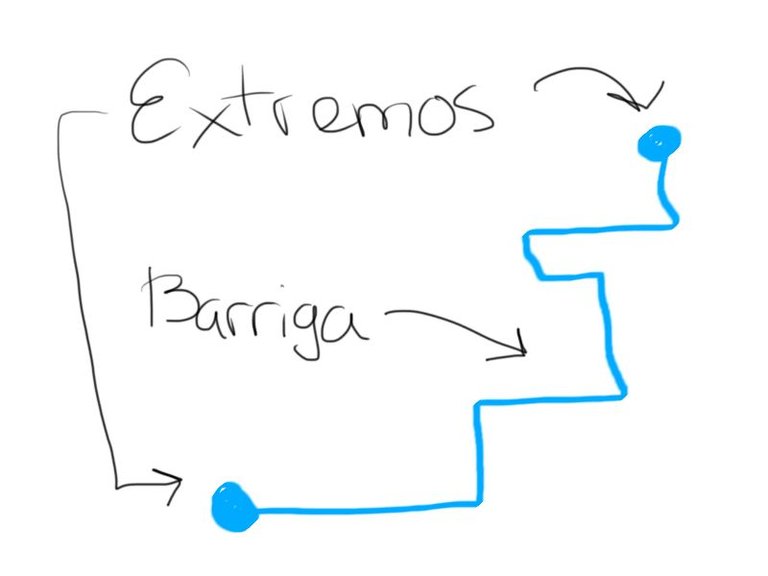
Tenemos que
- Ningún extremo puede tomar el lugar de un trozo de barriga
- No deben quedar espacios que no contengan o un extremo o una barriga en la retícula
Entonces, para ir transformando nuestras líneas rectas al puzzle original (o algún otro puzzle) debemos de modificar las líneas de una forma tal que respeten esas reglas. En principio, sólo podemos o estirar o encoger las líneas, que es simplemente cambiar de posición los extremos. ¡Pero no podemos hacer cualquier cambio! Porque si movemos un extremo a través de la barriga de otra línea, entonces habremos roto la primera regla. He aquí la conclusión final: hay que intercambiar extremo por extremo.
Es decir, debemos llevar a cabo dos acciones:
- Ver la retícula y analizar cuáles extremos de distintos colores comparten un borde (se encuentran a exactamente una casilla de distancia)
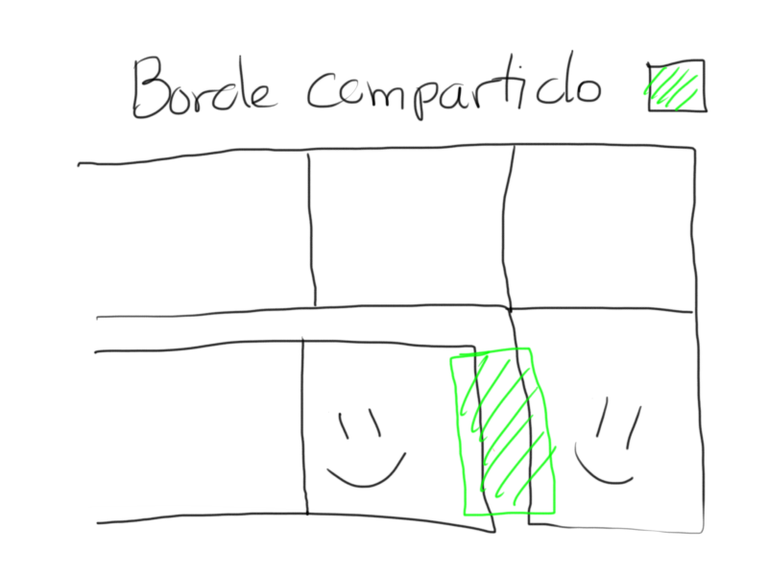
- Extender una de las líneas y encoger la otra, tomando el extremo de la línea extendida el espacio que deja el extremo de la encogida al ceder.
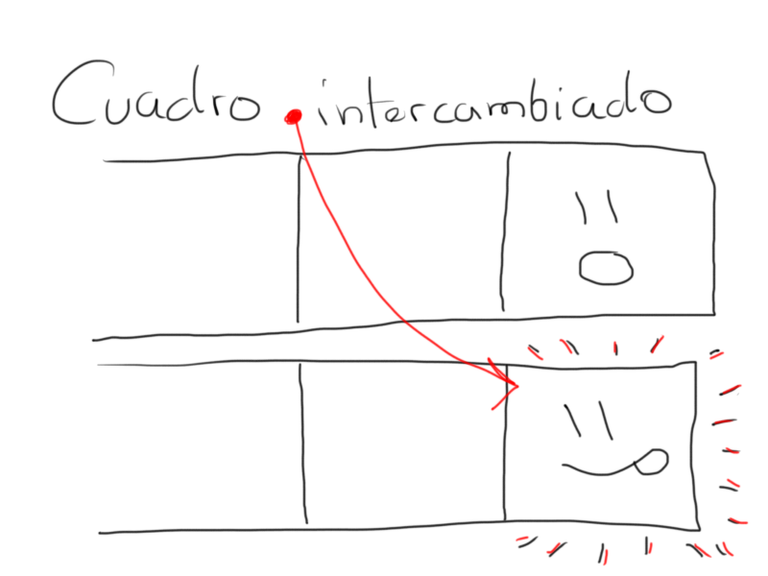
Si hacemos esto una, y otra, y otra vez, eventualmente llegaremos a un desastre de líneas… pero que jamás se cruzan. Eso es un puzzle de Flow :)
El Código
Una vez entendido el algoritmo, el código es bastante sencillo. Comencemos por lo primero: importar los módulos.
import numpy as np
import random
import colored
Usaremos random para generar números aleatorios, colored para darle color a nuestro resultado, y numpy solo para calcular normas de vectores (si no sabes de lo que hablo, quizá quieras leer esto primero). Les debo una advertencia: este código solo corre en Linux por el uso de colored, porque al parecer Windows odia ponerle color a su texto fácilmente.
Ahora, definimos unas cuantas variables como doble espacios de color:
re = colored.attr('reset')
na = colored.bg('0') + " " + re #El doble espacio entre las comillas es importante
a = colored.bg('1') + " " + re #resulta que el doble espacio se parece bastante a un cuadrado
b = colored.bg('2') + " " + re #en las terminales de Linux, entonces esto sirve
c = colored.bg('3') + " " + re #como truco para hacer cuadritos de color.
d = colored.bg('4') + " " + re
e = colored.bg('5') + " " + re
f = colored.bg('6') + " " + re
g = colored.bg('7') + " " + re
h = colored.bg('8') + " " + re
i = colored.bg('9') + " " + re
j = colored.bg('10') + " " + re
k = colored.bg('11') + " " + re
l = colored.bg('12') + " " + re
m = colored.bg('13') + " " + re
n = colored.bg('14') + " " + re
o = colored.bg('15') + " " + re
dic = [a,b,c,d,e,f,g,h,i,j,k,l,m,n,o]
Algunos parámetros del código y del puzzle...
n = 8 #Dimensión de la retícula
chain_limit = n-4 #Tamaño mínimo de línea
iter = 800 #Número de Iteraciones
Y ahora el motor del código; tres funciones importantes. Una para generar el estado inicial de la retícula...
def baseMatrix(dim): #Genera estado inicial de la retícula con lineas horizontales de logitud 'n'
A = []
for l in range(dim):
A.append([]) #Agrega 'dim' entradas vacías al nivel 0 de la lista
for i in range(dim):
for j in range(dim):
A[i].append([np.array([i+1,j+1]), dic[i]]) #Llena las sublistas del nivel cero con la información de cada línea:
#Un par coordenado junto a una etiqueta que indica a qué color pertenece;
#El principio y fin de esta lista son los extremos de la línea
#Seleccionar una lista del primer nivel de 'A' es lo mismo que seleccionar una línea entera
return A
... otra para hacer propiamente el proceso de intercambio de extremos ...
def edgeSwitch(A): #El código principal del generador: esta funcion alarga/encoge dos líneas con extremos que comparten bordes
#Primero, analiza cada línea:
sw = False
for i in range(len(A)): #Para cada fila...
if sw == True:
break
for k1 in range(-1,1): #Para cada extremo en la fila seleccionada...
if sw == True:
break
p = A[i][k1][0] #con 'p' siendo la posición del extremo seleccionado...
for j in range(len(A)): #Para todas las filas, excepto la i-ésima (que es la que seleccionamos)...
if sw == True:
break
if j == i:
continue
if len(A[j]) == chain_limit: #con longitud mayor al tamaño mínimo...
continue
for k2 in range(-1,1): #Para cada extremo de la segunda fila seleccionada...
if sw == True:
break
pprime = A[j][k2][0] #con 'pprime' siendo la posición del extremo seleccionado de la segunda línea...
if np.linalg.norm(p-pprime) == 1.0: #Si la distancia entre ambas posiciones es exactamente 1, entonces los extremos comparten borde.
n1 = np.random.rand() #Lanzamos una moneda, y si 'n1' es mayor que 0.5...
if n1 > 0.5:
A[j].pop(k2) #Quitamos el extremo de la segunda línea...
if k1 == -1:
A[i].append([pprime,A[i][0][1]]) #... y se lo agregamos a la primera.
elif k1 == 0:
A[i].insert(0,[pprime,A[i][0][1]])
sw = True
else:
continue #Si 'n1' no es mayor que 0.5, pues tomamos otra segunda línea
return A
... y dos finales, pues, para poder ver el puzzle (y su solución :P)
def flowPrinter(A): #Una función auxiliar para imprimir el puzzle
C = [] #Creamos una lista vacía...
for z in range(n):
C.append([na]*n) #y la llenamos con 'n' sublistas de 'n' entradas en negro ('na' es negro, segun la definicion de colores)
for i in range(len(A)):
for j in range(len(A[i])):
x = A[i][j][0][0] - 1 #Hallamos los índices de los extremos de cada línea...
y = A[i][j][0][1] - 1
C[x][y] = A[i][j][1] #... y sobreescribimos ese elemento en 'C' con el color correspondiente
s = ""
for k in range(n): #Finalmente, imprimimos a cada fila 'C' como una sola línea de caracteres.
for l in range(n):
s = s + C[k][l]
print(s)
s = ""
def flowPrinter_puzzle(A):
C = []
for z in range(n):
C.append([na]*n)
for i in range(len(A)):
for j in range(-1,1):
x = A[i][j][0][0] - 1
y = A[i][j][0][1] - 1
C[x][y] = A[i][j][1]
s = ""
for k in range(n):
for l in range(n):
s = s + C[k][l]
print(s)
s = ""
Finalmente, el código principal es tan simple como
flow = baseMatrix(n)
for step in range(0,iter):
flow = edgeSwitch(flow)
random.shuffle(flow)
flowPrinter(flow)
print('\n \n')
flowPrinter_puzzle(flow)
Ojo, ese random.shuffle(flow) es SUPER importante. Como edgeSwitch pasa por cada una de las filas de A de forma descendiente, el algoritmo le da cierta parcialidad a las filas que están primero. Con ese pedacito de código cambiamos aleatoriamente el orden de las filas para deshacer la parcialidad.
Y ya. Eso es todo. Con alrededor de 140 líneas de código logramos hacer un script que genera niveles de Flow :) Ahora veamos los resultados!
Resultados
Corriendo python3 flowgen.py para n=15, obtenemos lo prometido. Un nivel de Flow aleatorio :)

Pasando a n=8 y tomando iter=400obtenemos uno de 8x8.

¡Esos verdes y rojos, aunque se confundan, no son iguales! Es cuestión del procesado para mostrarlos en Steemit
Y finalmente, para los tontillos de la casa, uno 6x6 (vamos, que los 4x4 son triviales).
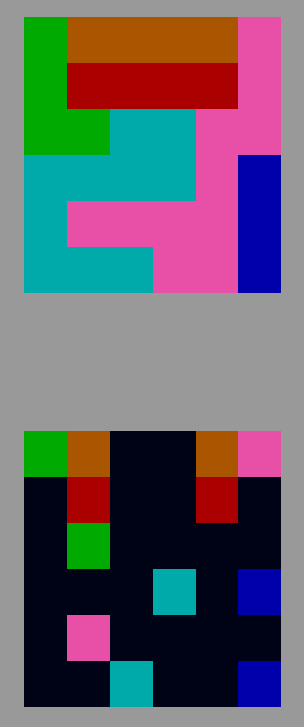
Comentarios Finales
La primera vez que corrí este código me topé con una sorpresa. Si iteres muy grande, cuidado: tendrásun montón de cuadrados. A medida que mueves más y más las líneas, se hace cada vez más probable que los extremos terminen atascados entre la barriga de otra línea y su propia "cola", haciendo un lindo cuadrado que no avanza jamás. Es solo una consecuencia del diseño del algoritmo. La solución es escoger un valor apropiado para iter. He encontrado que multiplicar por 10 la dimensión de la retícula basta como para "mezclar bien" las líneas. Otra cosa sobre ellas es que si el límite chain_limit es muy pequeño, tendrás líneas estúpidamente cortas (lo cual es indeseable; tú quieres lineas malévolas super enredadas (:< )
Sí. Ya sé lo que estás pensando: Samuel, tú me dijiste que empezaríamos con un puzzle de Flow, y que partiendo de líneas horizontales llegaríamos al mismo puzzle de Flow. Amigos, la vida es dura y la noche es oscura, y yo dije al principio que jamás llegué a dar con eso, que es esencialmente lo mismo que resolver un nivel de Flow (por razones de tiempo; la Uni a veces aprieta). Por ahora me conformo con poder generarlos, y reirme de saber que si hubiese hecho esto hace unos años atrás estaría revolcándome en dinero de microtransacciones. Pero bueno... hacer niveles de Flow de tamaño arbitrario sin dinero de por medio es igualmente divertido (¡aunque eventualmente se te acabarán los colores, o no podrás distinguirlos!)

Espero les haya gustado este post, que hayan aprendido algo, y por sobre todo lo demás, que salgan de aquí sintiendo que ustedes mismos pudieron haber inventado Flow (con un poquito de imaginación).
Si te gustaría que hiciése más posts de programación en español como éste, apoya mi contenido y envíame un upvote con buenos deseos, y deja un comentario abajo :)
Nos vemos pronto,
-SA

Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial-CompartirIgual 4.0 Internacional.