협업 필터링 (1)

콘텐트 기반 추천 시스템이 2000년대 초반 사용됐던 기술이라면 협업 필터링은 지금까지도 가장 널리쓰이는 추천 기술입니다. 아이템 유사성을 기반으로 추출한 특성을 사용하는 대신, 서로 다른 사용자들이 서로 다른 2개의 아이템을 평가한 유사성을 기준으로 추천합니다.

이에 따라 선호도 행렬을 이용하는 방법도 다릅니다. 콘텐트 기반 추천 시스템에서는 아이템 프로파일을 구성할 때 선호도 행렬의 한 열, 즉 하나의 아이템을 프로파일의 구성요소로 사용하지만, 협업 필터링에서는 선호도 행렬의 행, 즉 한 명의 사용자의 정보를 토대로 가장 비슷한 다른 사용자를 찾아 내고, 그 사용자가 좋아한 아이템을 추천합니다.

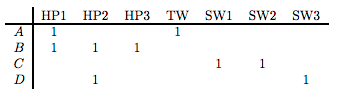
우선 사용자 유사성을 측정하기 위한 방법을 살펴보겠습니다. 선호도 행렬은 다음과 같이 주어져 있다고 가정합니다.

선호도 행렬 처리하기

데이터 라운딩(rounding)

평점이 주어진 선호도 행렬에서 3, 4, 5점은 상당히 유의미하게 좋아했던 아이템으로, 1, 2점은 보았더라도 좋아하지 않았던 아이템으로 평가할 수 있습니다. 그럴 경우 3, 4, 5점은 1으로, 1, 2점은 0으로 처리해 라운딩합니다.

데이터 정규화(normalizing)

앞서 시도한 정규화와 동일한 방법입니다. 사용자별 평균 평점을 구한 뒤, 각 점수에서 빼주는 방법입니다. 예를 들어 A 사용자는 3개의 아이템에 대해 총 10점을 주었으므로 평균은 10/3 입니다. 이에 따라 HP1, TW, SW1의 점수는 각각 2/3, 5/3, -7/3이 됩니다. 음수가 등장하게 되는 것입니다. 같은 방법으로 사용자 모두에 대한 정규화를 해본 결과는 아래와 같습니다.

사용자 유사성 측정하기

위의 방법을 다양하게 이용하여 선호도 행렬을 분석하기 좋은 형태로 바꾼 뒤에는 사용자 유사성을 계산합니다. 앞에서 다룬 것처럼 대표적으로 자카드 거리(Jaccard Distance)와 코사인 거리(Cosine Distance)를 다뤄봅니다. 선호도 행렬은 라운딩과 정규화 이전의 데이터를 활용해 보도록 하겠습니다.

자카드 거리의 계산식은

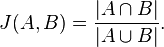(자카드 인덱스)

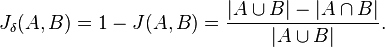
와 같습니다. A사용자와 B사용자의 자카드 인덱스는 n(A∪B) = 5, n(A∩ B)=1 으로 1/5입니다. 따라서 자카드 거리는 4/5가 됩니다. 마찬가지로 A 사용자와 C사용자의 자카드 거리는 1/2입니다. 즉, A 사용자와 C사용자가 더 유사성이 높은 것입니다.

하지만 이런방법에는 한계가 있습니다. 분명 A 사용자와 C 사용자가 더 유사하다고 결과가 나오긴 했지만, TW, SW1의 점수를 보면 두 사용자의 평점의 패턴이 다르다는 것을 알 수 있습니다. 오히려 A 사용자와 B 사용자가 HP1에 대해 높은 점수를 공통적으로 준 것을 알 수 있습니다.

이에 따라 코사인 거리를 계산해 봅니다. 앞서 다뤘듯, 식은 아래와 같습니다.

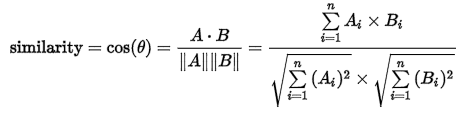(코사인각, 코사인 유사도)

코사인 거리 = 1- 코사인 유사도

물론 두 벡터의 내적값이 구해져야 하므로, 평점이 존재하지 않는 항목엔 0을 채워줍니다(안 본것을 저평점으로 계산하는 것에는 문제가 있을 수 있습니다).

A사용자와 B사용자의 코사인 유사도와 A사용자와 C사용자의 코사인 유사도는 각각

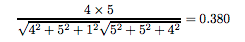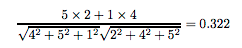
이와 같고, 따라서 코사인 거리는 A 사용자와 B사용자 사이가 더 짧아서 유사성은 더 높다고 볼 수 있겠습니다. 한편, 정규화를 통해 음수가 등장한 선호도 행렬에서는 코사인각의 방향성까지 고려할 수 있습니다. 두 사용자의 벡터가 반대방향을 가리키고 있는 경우 유사성이 떨어질 것이라 직관적으로 알 수 있습니다.

유사도 평가에 대해서 교재에서는 자카드와 코사인을 이용한 방법만 주로 다루었지만, 최근까지 보고된 논문에 따르면 엄청나게 많은 유사성 계산법이 있습니다. 저도 구현할 때 몇 개 더 만들어볼 생각인데, 구글링 했을 때 인용이 1000이상 나오는 Comprehensive Survey on Distance/Similarity Measures between Probability Density Functions라는 논문 링크 남깁니다.