Everything from sending credit card data over the Internet and keeping personal files secure depends on a formula from Number Theory, known as RSA encryption.

(Picture: http://www.itbusinessedge.com)
Here's a little refresher on prime factorization:
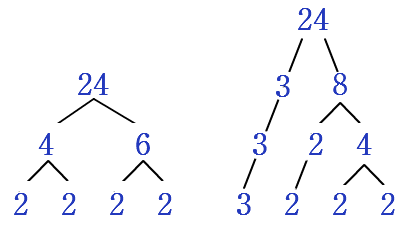
(Source: http://www.mathcaptain.com/number-sense/prime-factorization.html)
And we know, finding the prime factors for an arbitrarily large number becomes harder and harder to do as the number increases. If I gave you a number like 667 and told you to find the prime factors, you would have to run through the primes from lowest to highest (or highest to lowest) of 667 and start dividing. You could also memorize certain tricks, or you could write a program that does this for you. Python goes pretty far for these tasks, and it is easy to use. The point is however, that there is no algorithm, or set of instructions, that is a general solution to prime factorization problems. We are basically stuck with guess and check. To date there has been no system or pattern found in how frequently primes occur on the number line either.
Let me give you an example of RSA in action. If I came up with two missive prime numbers, say p1 and p2 and multiplied them together, I would have an even more massive number, call it N. And as I have described, there is basically no algorithm to factor the primes out of N besides just running through all of them. Let p1 = 2 and p2 = 7. Then N = 14. The next part relies on modular algebra. Given any number (ASCII messages or letters can easily be converted into binary strings of numbers). Let my message be the simple letter B, or 2 as a number. Then I'm going to raise 2 to the power 5, which is 32 and is my encryption key (e = 5). When you divide 32 by N (N=14) you get a remainder of 4. This 4 is our cipher (c = 4). It is what is send over the Internet or network. It doesn't matter who sees it because unless they have the decryption key (which is d = 11), they will be virtually unable to unscramble it into the original message. Of course I'm using small numbers for simplicity, but with large enough primes nobody could solve a problem like this in their entire lifetime using binary computers...unless you are freaking Rain Man.

Now to decrypt, let's take the cipher 4 and raise it to the power of the decryption 11, and then take mod 14 (or find the remainder after dividing by 14) and you get 2! Our original message has been revealed.
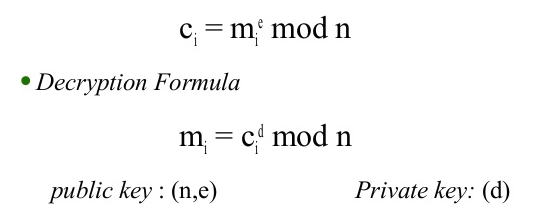
Here are the more technical aspects of RSA.

Take two prime numbers p and q, as large as your computer will allow, and multiply them together to get N. Keep these two primes hidden. If they are revealed, then your code can be cracked. Then do the Phi Function (from Number Theory) on the product of the primes. The formula is Phi = (p-1) x (q-1). Phi counts the number of co-prime numbers of N. Co-prime means that there are no common factors. So with p=2, q=7, and N=14, the co-prime numbers are 1,3,5,9,11, and 13. Take all integers less than or equal to 14 and remove all numbers that have common factors with 2 and 7. So Phi adds up to 6.
Now for the encryption e, make sure it is greater than 1 and less than 6 (The Phi Number). We have the options of 2,3,4, and 5. But make sure e is co-prime with N, and only 5 does not have a common factor with 6 (excluding 1 of course). So e = 5.
Now for d (the decryption key) make sure that d times e mod Phi is congruent to 1. In other words, find a number so when you multiply d and e together and divide it by Phi it has a remainder of 1. I could choose d = 5, since 5 x 5 = 25 and divided by 6 has a remainder of 1, but I am going to pick d = 11 to make it a little harder, and 5 x 11 = 55 and has remainder 1 upon division by 6. This d is your private key and must only be accessible to the user receiving the message. It doesn't matter if others can see the encryption key. Even if they could, it would be virtually impossible for them to decode the message.
(Picture: http://www.giuseppeurso.eu/en/asymmetric-rsa-encryption-in-java/)

So there you go! That is RSA encryption. This is an essential tool for computer scientists and has massive implications for financial transactions, securing private data, and having a valid system of payments unable to be spied on and exploited.
I thought this was really cool when I first heard about how prime numbers are used for encryption. From my understanding, won't quantum computers destroy this someday due to the way they work?
Yes! or at least maybe. I'll post content on quantum computers in the weeks to come. I took a class on it in college and want to break it down for people here.
That would be great. I watched a few videos that explain how they work and think it is really fascinating. I know they are still in their infancy but they could really revolutionize technology.
I am curious as to what are the benefits. What benefits is there to any one who breaks this algorithm. Also is there a prize given to do so.
By the way I like your presentation. And your "Rain Man" reference had me on a good laugh. Its so true.
You need to check out this blod post <voice-of-apollo>. Very interesting discover that you might have the ability to understand and appreciate. Plz give feedback comments.
https://steemit.com/cryptography/@becomethreality/a-new-mathematical-formula-for-public-key-cryptography-discovered