Run the Math
Functions
By Bryan Bartlett
Previous-----Index-----Next
Answers to Previous Lecture
A number belongs to the set of Rational Numbers Q if it can be written as a fraction p/q, where p and q belong to the set of Integers Z. In this example, let us let x = 0.125. This means 1000x = 125, which implies x = 125/1000 125 and 1000 are both integers so 0.125 = 125/1000 must be in the set of Rational Numbers. And since all Rational Numbers belong in the set of Real Numbers, 0.125 must be a real number.
This one is a bit trickier. For those that don't know, the √-1 = i (imaginary number), which make up the Complex Number system (we will get into it later.) Now, i is not in N. There is no way you can start with 1 or 0, and add 1 continuously to get to i. similarly, since Z is all Integers, you cant start with 0 and subtract 1 continuously to get to i. There is also no combination of integers p and q that will get i either. What about irrational numbers? If you start with any rational number, and keep adding a digit to the end of the decimal, you will always have a number that is real, but no matter how many times you add a digit, you will never equal i. Thus, i is not in the set of Real Numbers
To solve for x, we need to divide both sides by -4. But, because it is a negative, the sign switches, so -4x < 8 ≡ x > -2. This means x is always greater than -2, without limit. The bracket notation then would be (-2,∞)
This tells us that x is between 3a2 - 4 and a - b, not including a - b. the less than or equal to symbol and the less than symbol tell us this. so, it would be [3a2 - 4,a-b)
This tells us that x<a+5, with no lower limit. we would state then that {x|x<a+5}
Functions
A function is defined as a correspondence that associates each element x of some set A with a unique element y in set B. OK, this may look complicated, but what it is saying is that if we have a set of numbers we can use for x and put it into a function, it will result in a single value. For example, all of the following are functions written in different ways
y = 5x + 4
f(t) = t2 - ln(t)
g(x) = sin(2x)
h(y) = ey
Notice the use of h(y) on the final example. This still is a function, because it is with respect to y: That is y is the independent variable in that equation. Usually we will avoid the use of y as a independant variable to avoid confusion. The letters f,g,and h are arbitrary labels to the equations that allow for a simpler writing. Once you have declared the equations, you can simply use f, g and h on their own, and still refer to f(t), g(x) and h(y).
The easiest way to determine if something is a function is the "Vertical Line Test". If you were to graph the function, and there was any point you can draw a vertical line and cross it in more than one place, then it is not a function.
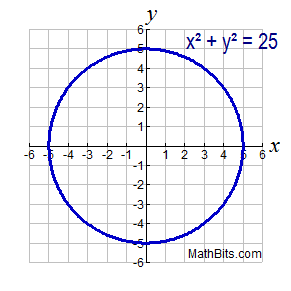
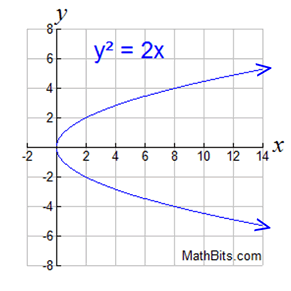
Images from Math Bits
Neither of the equations above would be functions, because one x value will give you multiple values for y. However, taking the parabola as an example, the equation y = -√x WOULD be a function, it would be the bottom half of that parabola.
One to One functions are functions that, for every x, there is a unique y, and for every y there is a unique x. You can easily tell a one to one function by applying a horizontal line test! A function has to pass both vertical and horizontal line tests to be considered one to one.
Operations on Functions
Operations on functions are very easy, they are very similar to regular mathematical operations. Given functions f, g and a constant c
- The sum (f + g)(x) = f(x) + g(x)
- The difference (f - g)(x) = f(x) - g(x)
- The product (fg)(x) = f(x)g(x)
- The quotient (f/g)(x) = f(x)/g(x), where g(x) ≠ 0
- The scalar function (cf)(x) = cf(x)
Composite Functons
Composite functions use an open dot notation like this (f ◦ g)(x). What this means is you take f(g(x))... that is you evaluate g(x) and then use that as x in f(x).
Example:
Let f(x) = x + 1 and g(x) = x2
(f ◦ g)(x) = f(g(x)) = f(x2)
Replacing all x in f(x) with x2 gives (f ◦ g)(x) = x2 + 1
Note, that (f ◦ g)(x) does not necessarily equal (g ◦ x)(x). Using above example:
(g ◦ f)(x) = g(f(x)) = g(x + 1)
Replacing all x in g(x) with (x + 1) gives (g ◦ f)(x) = (x + 1)2 = x2 + 2x + 1
Inverse Functions
Inverse functions, when graphed, are mirror images of a function, as viewed from the line
y = x.

Image from Sparknotes
When you want to calculate what the inverse function is, you are really just swapping out the independent and dependent variables.
Let f(x) = 3x3 + 4
To find the inverse function, we are really solving for f(f-1(x)) = 3f-1(x)3 + 4
Note, that f(f-1(x)) actually equals x, which gives us x = 3f-1(x)3 + 4. You can see why you can just replace f(x) with x and replace x with f-1(x). All we do now is solve for f-1(x).
x - 4 = 3f-1(x)3
(x - 4)/3 = f-1(x)3
f-1(x) = 3√[(x - 4)/3]
And there you go! If you have any questions, please put them in the comments below!
Assignment
- Is f(x) = cos(x) a function? Is it 1 to 1?
- Is f(x) = x5 + 4x2 - 3 a function? Is it 1 to 1?
- Is y3 = x - 1 a function? Is it 1 to 1?
- Let f(x) = x2, g(x) = x + 3, and h(x) = x - 3. What is ((h*g + g2)/2-f)(x) Work it out step by step using standard order of operations, and function operations.
- If g(x) = x + 3 and h(x) = x - 3, what is (g ◦ h)(x)?
- We showed above that if f(x) = 3x3 + 4,then the inverse is
f-1(x) = 3√[(x - 4)/3]. Show that (f ◦ f-1) = x
Hi, I am the new curator for @math-trail, a community dedicated to promoting the best articles on mathematics in its widest sense, including educational and cultural aspects.
I just upvoted your post - hope to see more in the future.
If you like to write about mathematics, then please follow @math-trail and I will follow you back and look forward to see fresh new content.
If you enjoy reading about mathematics, then please follow me so that you will receive the best content in your personal feed.
I am not a bot! Thanks!
Followed you, and I will be posting the next segment tommorrow I hope! Thank you for the support!