The Holographic Principle, unusual gyroscope, and control of gravity
In modern times in known works, It was demonstrated the existence of a deep connection between gravity and entropy [1, 2, 3]. More recently, fundamental ideas such as the Holographic Principle [4, 5] аnd the entropic gravity E. Verlinde [6], also known as emergent gravity, is a theory in modern physics that describes gravity as an entropic force.Today the Holographic Principle - is hundreds of theoretical works by famous world-class physicists: G. 't Hooft, L. Susskind, J.D. Bekenstein, E. Verlinde, J.M. Maldacena, R. Bousso ... . Already there are experimental studies confirming the operation of the Holographic Principle [7], [8]. Since 1997, more than 10,000 works have been published supporting this idea.
MGEF
The MGEF (Module Generator of Entropic Forces) project on base unusual gyroscope (UG) exists for the experimental verification of the Holographic Principle. If the Holographic Principle works, then it is possible to artificially create the long-range gravitational forces and this will allow us to control gravity and have many exciting apps without violating the fundamental laws of physics.
What is UG?
This is a small electromechanical device that can occupy a tenth of your desk. The spherical rotor UG have magnets and rotates in a vacuum inside the spherical stator with inductors under the control of the computer (there are sensors and drivers for producing forced oscillations of the rotor). Name UG is justified by the fact that its rotor produces complete forced oscillations around three fixed axes per cycle. Here the overwhelming majority of experts will oppose. According to Euler's rotation theorem, simultaneous rotation along a number of stationary axes at the same time is impossible. However, I ask attention, for of full turnover of a physical body (or rotor) around three fixed Cartesian axes per cycle - possible. "Cycle" this keyword. In the scientific literature, there is no description of such fluctuations. We can use one a simple parametric equation of angular displacement of the point on the rotor according to the laws of harmonic oscillations.
(θx=Cosθ
(θy=Sinθ
(θz=-Sinθ,
where θx, θy, θz serial angular displacement of any pre-selected point on the rotor around the corresponding axes: where parameters: θ= πt and -1 ≤ t ≤ 1; θ is geometrical angle admeasured by arbitrary and preselected direction of angular rotations. The equation is given parametrically, and it is applicable for any radius of the rotor. We can We can ask max accuracy of the angular displacement if Δt → 0.
As soon as a new type of gyroscope - UG was invented and testing on the simulator, the question arose: what new properties can it have?
The first thing that catches your eye, looking at a very simple equation of the rotor's motion, is that the oscillations of the rotor are coherent. Since the phase difference of the oscillations is a constant. In addition, using a simulator, we can observe a fixed interference pattern from accelerates (α) related to fixed Cartesian coordinates. We can see six groups of diametrically arranged rotational accelerations per cycle. If we calculate all possible directions of such coherent oscillations of the rotor, then their number will be exactly 60.
The equivalence principle
The equivalence principle tells us that we cannot distinguish between inertial and gravitational mass by experiment. Einstein invented an experiment with an elevator. The elevator is infinitely remote from the gravitating bodies and moves with acceleration. Then all the bodies in the elevator will be under the force of inertia and put pressure on the elevator base surface. That is, the bodies will have weight. If the elevator is not moving, but hanging over the gravitating mass in a homogeneous field, all bodies will also put pressure on the elevator base surface. Thus, it is not possible to distinguish between these two forces in the elevator. Therefore, all mechanical phenomena will occur equally in both elevators. Einstein extended this statement to all masses of physical bodies in the universe. If we are looking for a way to control gravity and Einstein's axiom allows us not to distinguish between the forces of inertia and gravity, we must take advantage of this and involve the fact that there are forces of inertia which depend on speed. For example, it is the Coriolis force. The Coriolis force deflects the body from the rectilinear motion if these bodies are in a rotating non-inertial frame of reference.
A new type of gyroscope has coherent oscillations of the rotor

UG is a fundamentally new type of gyroscope, which differs from the conventionally powered gyroscopes not merely by the absence of mechanical axes and the absence of the gas cushion, but also by the coherent oscillation of the spherical rotor in the stator vacuum cavity. While the rotor of a conventionally powered gyroscope makes a complete rotation around the same axis per one oscillation cycle, the UG gyroscope rotor compelled quickly rotates around three axes (Ox, Oy, Oz). This is its conceptual difference from any other powered gyroscope and this feature is reflected by the author of this text in the formula of the relative patent application. The levitation of the rotor within the stator is achieved by suspending it in the active electromagnetic suspension. Typically, a gimbal is used in the three-axis gyroscopes, which allows free rotating of the rotor relative to the three axes, and this is what makes them akin to UG. Forced and full oscillations of the rotor UG around three axes per cycle - this is its fundamental difference from a conventional gyroscope.
Thus, per a cycle of coherent oscillations, the rotor UG makes a complete revolution around one fixed point - is the geometric center, the mass center and the center of the accelerations and around the three axes of the Cartesian coordinates.
For example:
We are given accuracy Δt = 1/360. This means that we began will make the angular displacements of any point on the surface of the rotor rotation about by one degree, for example, according to the law (Cosθ) around the fixed axis x in the constant minimal time interval. In the next equal and minimum time interval, we can produce angular displacements about the axis y, but already according to the law (Sinθ) and, respectively, z (- Sinθ). But since there are still about 359 degrees for every axis left until the end of the cycle, we continue with such triads, which eventually will end simultaneously for all functions, since the phase difference is constant. We have received a cycle of coherent oscillations. We do not yet need to know how the rotor points behave, what are their trajectories. Functions alternate and there are six groups of directed (Instant) rotational accelerations associated with fixed Cartesian coordinates. In space and during the cycle, they occupy permanent positions. We obtained coherent oscillations of the elements of mass in a vacuum.
The Coriolis force
Our objective is to obtain the maximum amount and magnitude of the Coriolis force acting on the elements of the mass of rotor. The magnitude of the Coriolis forces depends on the rotor angular speed. We can assume that superposition of the Coriolis forces obtained in this way is equivalent to a fictitious "gravitational" field acting on each rotor element of mass. Since the Coriolis forces are equal to each other and orthogonal, their resultant is zero, and the rotor center of mass remains stationary. We can increase these forces by increasing the rotor speed.
But, it is very important that we may simultaneously displace all points (all elements of mass), for example, around two of the three fixed Cartesian coordinates artificially on short time producing decoherence. And yes, we can make this at the end of the cycle. At the same time, we do not violate Newton's third law as long as we do not while the claim that the rotor center of mass should change its position in space in such closed system.
Another thing is if the holographic principle works, which is indirectly confirmed in experiments. This allows us we should extend the size of the closed system to its maximum size, the holographic screen of the universe.
Another thing is if the holographic principle works, which is indirectly confirmed in experiments. This allows us we should extend the size of the closed system to its maximum size, the holographic screen of the universe.
A difference of temperature in different directions
Commensurate in scale with the Holographic Principle was the discovery of the anisotropy of the Universe in 1992 (anisotropy of cosmic microwave background - CMB) this the difference of temperature in different directions on the sky [9]. Experimentally confirmed by the anisotropy of the CMB and the discovery of coherent acoustic waves in the early Universe is of great importance not only for cosmology but for the whole of natural science as a whole. It can be said that large-scale three-dimensional sound coherent oscillations act before recombination period and ended after 379,000 years, but did not disappear completely, and recorded big scale of the global gradient of temperature on the holographic screen (according to the holographic principle, the projection of all phenomena occurs without loss of information). To investigating thermodynamics on the holographic screen, we must take into account the impact of it's of global temperature anisotropy on the dynamics the projections. Holographic Principle can reveal a new holographic mechanism for the generation of masses of particles and for all known forces and interactions as an entropic force.
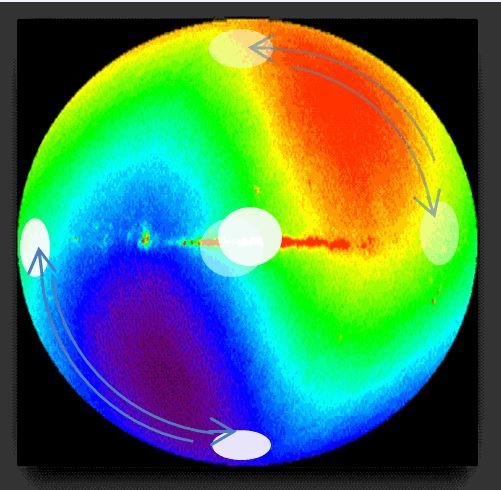
http://lambda.gsfc.nasa.gov/product/cobe/
Control of gravity
Approximately half of the global temperature gradients on the holographic screen of the universe are different from each other, so two of the four groups of the entropy gradients (a half of them), due to the movement of the rotor elements of mass (during displacement the projections), experience a different interaction with these areas. A large-scale breaking of symmetry on the holographic screen, and the result of accelerating elements of mass during displacement lead to a directional entropic force that is applied to the geometric center (for a spherical rotor, this is the center of mass which coincides with its geometric center).
We can investigate device – UG in which gravity arises as a consequence of entropy.
According to the Holographic Principle, the change in this entropy when the matter moves leads to the entropy force that assumes the guise of gravity.
Fg=ΔTΔS,
where Fg is the gravitational force, ΔT is the temperature gradient on the cosmological horizon, ΔS is the entropy gradient resulting from the matter displacement and/or displacements on the holographic screen of the projection of the phenomena taking place in three-dimensional space ΔS ∼ α. After transformations, we arrive at Newton's second law [6], and it means that the gravity can be controlled without exotic masses and energies. Thus, the integral gravity effect is determined by a variety of entropy forces interacting with the large-scale (global) dipole anisotropy represented by the temperature at the holographic screen of the universe. Gravity is a thermodynamic phenomenon. A series of generated controlled and directed gravity forces allows us to perform shifting of the entire UG structure in space in any chosen direction in a nonreactive way. This means that for one point - center and for all points, i.e., the UG rotor center of mass, the gravity, for example, the gravity of the Earth, can be fully compensated and/or overcome.
Today, numerous experiments with rapidly (7000 rpm) rotating of mass in vacuum demonstrate long-range forces in 2.5 N. The idea that gravity force can be thought of as an entropic force is considered in the experiment [10].
Conclusions
If we consider all possible directions of coherent oscillations of the rotor UG, then their number will be exactly 60. This number is in accordance number of elementary particles the Standard Model. And, indeed, after a boot in a certified simulator, an extremely simple formula, describing the dynamics of the rotor UG, on the computer screen in isometrics, one can observe the appearance of a spherical screen and the dynamics and properties of the projections of elementary particles.
Holographic Principle concludes that: gravity is explained as an entropic force. The equivalence principle leads us to conclude that it is actually this law of inertia whose origin entropic. This thermodynamics on screen, arising from the statistical behavior of microscopic degrees of freedom associated with a global temperature anisotropy and localized on the holographic screen of the Universe. Thus the force of gravity and his long-range is not postulated but derived from a holographic scenario.
As a result of the interaction of the gradient of the entropy projections particle arising entropic force applied to the geometric center of the particle. Therefore, this mechanism is maybe responsible for the appearance of a mass. A result of the encoding information on the holographic screen appears mass/energy, gravity, and space-time itself. UG can be used for a detailed study of this assumption.
The series generated in UG directed long-range gravitational forces leads us to be able to control gravity.
UG device can answer the question: Does the Holographic Principle is valid, according to which the physics of our three-dimensional space-time is equivalent to the physics with the two-dimension of the hypersurface.
We have a simple equation of motion for any arbitrarily taken point in the universe. The equation which on the certified simulator demonstrates many properties of the particles of the Standard Model and the place where our three-dimensional world really exists - two-dimensional spherical holographic screen (this is an optical hologram property when each pixel of the hologram carries information about all objects). The work UG is described by the same equation. This means that we are on the right track, experimental data confirm this.
Scientific visualization confirms the need for an urgent prototyping of the model UG. Details on my site: www.isan.com.ua
References:
[1] J. M. Bardeen, B. Carter, and S. Hawking, “The four laws of black hole mechanics,” Commun.Math.Phys. 31 (1973) 161–170.
[2] J. D. Bekenstein, “Black holes and entropy,” Phys.Rev. D7 (1973) 2333–2346.
[3] S. Hawking, “Black Holes and Thermodynamics,” Phys.Rev. D13 (1976) 191–197.
[4] L. Susskind, “The world as a hologram,” J.Math.Phys. 36 (1995) 6377–6396, arXiv:hep-th/9409089 [hep-th].
[5] G. ’t Hooft, “Dimensional reduction in quantum gravity,” arXiv:gr-qc/9310026 [gr-qc].
[6] [Verlinde, 2010] Erik Verlinde. "On the Origin of Gravity and the Laws of Newton". http://arXiv:1001.0785v1 [hep-th].
[7] Margot M. Brouwer, Manus R. Visser, Andrej Dvornik, Henk Hoekstra, Konrad Kuijken, Edwin A. Valentijn, Maciej Bilicki, Chris Blake, Sarah Brough, Hugo Buddelmeijer, Thomas Erben,Catherine Heymans, Hendrik Hildebrandt, Benne W. Holwerda, Andrew M. Hopkins, Dominik Klaus, Jochen Liske, Jon Loveday, John McFarland, Reiko Nakajima, Cristóbal Sifón,Edward N. Taylor " "First test of Verlinde's theory of Emergent Gravity using Weak Gravitational Lensing measurements"https://arxiv.org/abs/1612.03034
[8] Niayesh Afshordi, Claudio Corian, Luigi Delle Rose, Elizabeth Gould, and Kostas Skenderis " Observational Tests of Holographic Cosmology"arxiv.org/pdf/1607.04878v2.pdf
[9] George F. Smoot "Cosmic microwave background radiation anisotropies: Their discovery and utilization" REVIEWS OF MODERN PHYSICS, VOLUME 79, OCTOBER–DECEMBER 2007.
[10] V. N. Samokhvalov “Non-electromagnetic Force Interaction in Presence of Rotating Mass in Vacuum,” [International Journal of Unconventional Science] 1(1), pp. 6-19, 2013 (Article received: 18 Nov 2012; Article accepted for publication: 23 Apr 2013) http://www.unconv-science.org/en/n1/samokhvalov/
Hi! I am a robot. I just upvoted you! I found similar content that readers might be interested in:
https://www.facebook.com/groups/52897964984/
I have similar content that readers might be interested in: https://www.facebook.com/groups/Unusualgyro/