Hey all met me, shared an important science for us to learn
How our eyes can see the light and how much light that we can see and why we distinguish a color. There is an article that I found and interesting for me to read it and you all need to see this is how our eyes can see the color
The human eye contains two types of receptors that respond to light: cones and rods. The rods are most responsive in low light conditions. While they do not provide any information regarding color, the rods are sensitive to the intensity of the light and provide a "black and white" night vision. They also provide our best motion detection and peripheral vision. Conversely, cones are most responsive in bright light and are sensitive to color. There are substantially more rods (120 million) than cones (6 to 7 million) in the human eye.
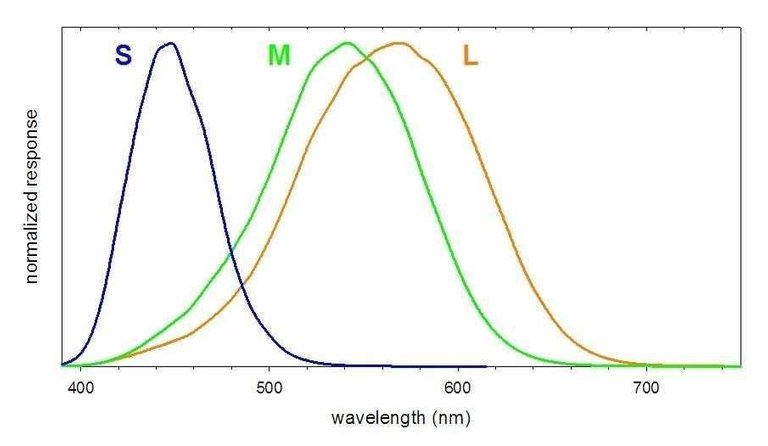
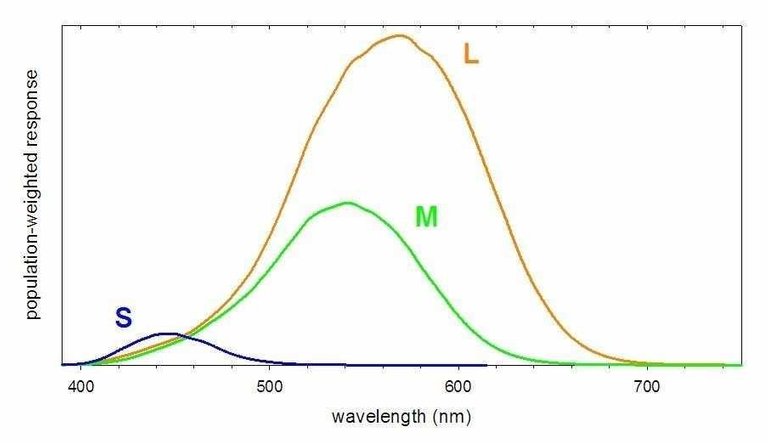
>The perception of color results from our brain processing the combined responses of the S, M, and L cones. Thus humans have trichromatic vision, that is, vision based upon three primary color responses. Color blindness is attributable to the missing or anomalous response of one or more of the cones. Dichromacy is a color blindness in which only two of the three types of cones function correctly. If the M cones, which are most sensitive to green light, are missing or nonfunctional, the disorder is called deuteranopia and the individual is unable to distinguish between red and green light. Protanopia is a disorder where the L cone is missing or nonfunctional and the individual is unable to perceive the color red. The very rare disorder tritanopia is associated with the absence of S cones, rendering the individual unable to perceive the color blue. The rendering and representation of color is a complex undertaking. One complication is that not all S (or M or L) cones are identical. For two individuals, there are chemical variations in a given type of cone that produce small variations in the response curve. Moreover, studies have found evidence for tetrachromic vision in some individuals (primarily women). These individuals appear to have a fourth cone, with a response between those of the M and L cones, that provides for greater differentiation of color than is possible with only three types of cones. Thus the perception of color varies somewhat between individuals. (This variation is particularly significant for individuals possessing some form of color blindness.)

The rendering of color by devices introduces its own difficulties. Numerous color models exist, and perfect conversion between models is not always possible. Even when two devices employ the same color model, the resulting colors may vary. Different "red" phosphors have slightly different emission spectra, and none are perfectly monochromatic. Users are also able to manually adjust the color balance of a monitor, thus altering the output. The situation is especially problematic for printers, where each manufacturer employs a proprietary set of inks. Please take these issues into account when pondering the colors shown on this page. Choose a different monitor, and you will see slightly different shades. A printed copy of this page will show still different shades, and the shades may vary significantly from one printer to the next. The color model employed below is a simple RGB model meant only to illustrate a few basic princples relating absorbance spectra to colors.
There is no unique way to map a specific wavelength to a specific color. Recall that color is in part perception. The image below provides an approximate representation of the color associated with each wavelength of light in the visible region. Below 400 nm and above 750 nm, the colors fade to black, because the human eye is unable to perceive light outside these bounds.
Source

Color in Gems
With these caveats in mind, we are finally able to answer the question: Why is a ruby red?
***Exercise*** In this exercise, you will be shown absorbance and transmittance spectra. * Examine the absorbance spectrum to determine the wavelengths (and thus colors) of light absorbed by the sample. * Examine the transmittance spectrum to determine the wavelengths (and thus colors) of light that reach the eye. * Predict the color of the sample. * After you have made your prediction, click on the "Show Color" button to see a reasonable (though not unique!) RGB representation of the color. >Consult the color wheels and the visible spectrum to assist in understanding how a given absorbance spectrum produces a given color. When the cursor is over a spectrum, press the left button to see the position of the cursor. This feature will aid in reading the wavelength.
Examine Samples A through I, each of which have a single absorbance maximum.
- What colors can be obtained with a single absorbance maximum?
- Why is it not possible to obtain any of the primary colors (red, green, or blue) when a single peak appears in the absorbance spectrum?
Examine Samples J through P, each of which have two distinct absorbance maxima. - What colors can be obtained with two absorbance maxima?
What must the absorbance spectrum look like in order to obtain the following colors? After you have reached a conclusion, examine the indicated Sample to test your prediction.
- Magenta Sample E
- Orange Sample Q
- Yellow Sample R
- Cyan Sample S
Hopefully this post is useful for us all and hopefully you like this article
And we already know together how much light we can see and a color
- Jane C. Arifin is a physicist. He holds a master's degree in photonics from Abbe School of Photonics, Friedrich Schiller University in Jena, Germany, in 2013. He is currently active in Science Workshop "teaching" science through experiments.
source
:http://www.chm.davidson.edu/vce/coordchem/color.html Printers, on the other hand, employ a subtractive color model. The paper is originally white (it reflects all colors). Ink is added to the paper to absorb specific components, removing them from the reflected light. A common subtractive color model is the CYM model, which is illustrated in the color wheel at the right.
Outside the three circles, the appearance is white, because all colors are present. Within each circle, a primary color (red, green, or blue) is removed. If the red component is completely removed, the result is cyan (lower left circle). If all of the blue component is removed, the result is yellow (top circle), and if all of the green is removed, the result is magenta (lower right circle). In places where the circles overlap, more than one primary color is removed. If red and blue are removed (application of cyan and yellow inks), the result is green, which is the only remaining primary color. If all three primary colors are removed (center of the wheel where all three circles overlap), the result is black.
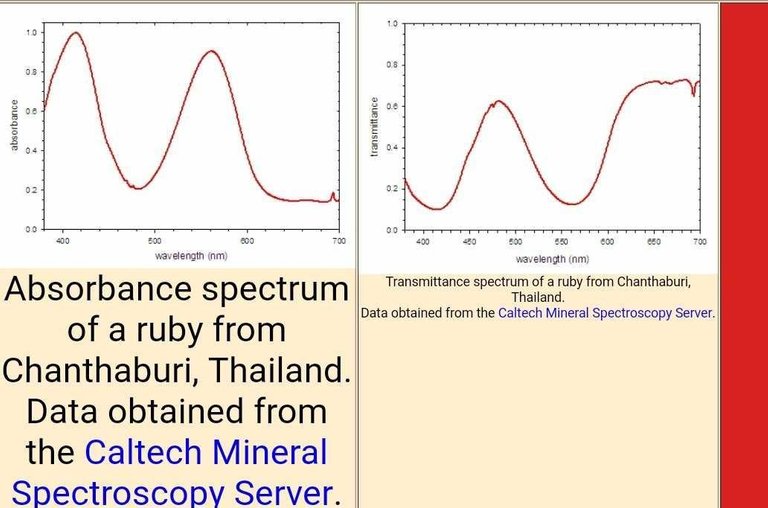
The absorbance spectrum of a ruby is shown at the lower left. The number and positions of the peaks in the spectrum is determined by the electronic structure of the compound, which in this case depends upon the identity of the metal and the identities, number, and geometry of the surrounding ions. Crystal field theory may be used to predict the electronic structure and thus the absorbance spectrum.
Printers, on the other hand, employ a subtractive color model. The paper is originally white (it reflects all colors). Ink is added to the paper to absorb specific components, removing them from the reflected light. A common subtractive color model is the CYM model, which is illustrated in the color wheel at the right.
Outside the three circles, the appearance is white, because all colors are present. Within each circle, a primary color (red, green, or blue) is removed. If the red component is completely removed, the result is cyan (lower left circle). If all of the blue component is removed, the result is yellow (top circle), and if all of the green is removed, the result is magenta (lower right circle). In places where the circles overlap, more than one primary color is removed. If red and blue are removed (application of cyan and yellow inks), the result is green, which is the only remaining primary color. If all three primary colors are removed (center of the wheel where all three circles overlap), the result is black.
The absorbance spectrum of a ruby is shown at the lower left. The number and positions of the peaks in the spectrum is determined by the electronic structure of the compound, which in this case depends upon the identity of the metal and the identities, number, and geometry of the surrounding ions. Crystal field theory may be used to predict the electronic structure and thus the absorbance spectrum.
 [Source](www.source)
One may regard the absorbance spectrum as a subtractive color scheme. If white light is shown on the gem, the absorbance spectrum indicates which wavelengths of light are removed. In this case, there are strong bands centered at 414 and 561 nm. These wavelengths correspond with blue and yellow-green light, respectively. For the most part, these colors are not present in the light reaching ones eyes.
An alternative way to express this concept is to recognize that the spectrum of light reaching the eye is the product of the spectrum of the incident light (white light) and the transmittance spectrum. For this ruby, the transmittance spectrum has a peak at 481 nm and a broad plateau past 620 nm. (Note that there is significant attenuation of the light across the entire spectrum.) Thus only light with wavelengths near 481 nm (cyan) and greater than 620 nm (red) reach the eye. The box to the right of the transmittance spectrum approximates the color associated with these spectra.
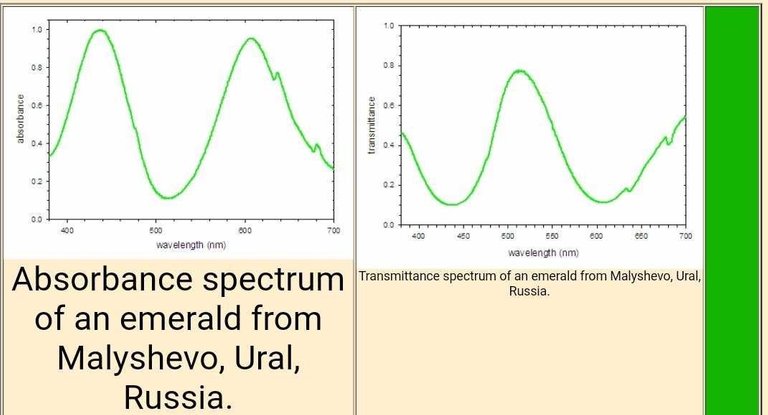
A similar analysis of the spectrum of an emerald is possible. The absorbance spectrum (below at left) shows strong bands at 438 and 606 nm, which remove blue and orange light, respectively. The light that is not absorbed is shown by the transmittance spectrum, which indicates the dominant band of light reaching the eye is centered at 512 nm (green light) with smaller contributions from the far blue and red portions of the spectrum. This combination of wavelengths produces a deep green color.
[Source](www.source)
One may regard the absorbance spectrum as a subtractive color scheme. If white light is shown on the gem, the absorbance spectrum indicates which wavelengths of light are removed. In this case, there are strong bands centered at 414 and 561 nm. These wavelengths correspond with blue and yellow-green light, respectively. For the most part, these colors are not present in the light reaching ones eyes.
An alternative way to express this concept is to recognize that the spectrum of light reaching the eye is the product of the spectrum of the incident light (white light) and the transmittance spectrum. For this ruby, the transmittance spectrum has a peak at 481 nm and a broad plateau past 620 nm. (Note that there is significant attenuation of the light across the entire spectrum.) Thus only light with wavelengths near 481 nm (cyan) and greater than 620 nm (red) reach the eye. The box to the right of the transmittance spectrum approximates the color associated with these spectra.
A similar analysis of the spectrum of an emerald is possible. The absorbance spectrum (below at left) shows strong bands at 438 and 606 nm, which remove blue and orange light, respectively. The light that is not absorbed is shown by the transmittance spectrum, which indicates the dominant band of light reaching the eye is centered at 512 nm (green light) with smaller contributions from the far blue and red portions of the spectrum. This combination of wavelengths produces a deep green color.
 [Source](www.source)
[Source](www.source)