Hello Steemit friends. I hope you all are having a nice week. In this post I derive the theoretical model for gasoline engine thermal efficiency. We will not need any fancy calculus or trigonometry. Instead we will use basic algebra, and a little knowledge of thermodynamics.
Lets get started. Most cars on the road today are power by internal combustion engines using the Otto cycle, named after Nikolaus A. Otto. There are multiple measures of engine efficiency, but this post will focus on thermal efficiency. Here is a quick overview of the different types of engine efficiencies.
1) Thermal efficiency: The ratio of the engine output to the input energy of the fuel
2) Volumetric efficiency: The ratio between the actual engine air flow and the maximum possible engine air flow
3) Mechanical efficiency: The ratio of the engine output to the power produced by the cylinders
4) Specific fuel consumption: The ratio of the fuel mass flow rate to the output power
First we will go over the operation of the Otto cycle, then to keep the math simple, we list the assumptions require to make an ideal Otto cycle, and then finally we derive the theoretical model for gasoline engine thermal efficiency. As complex as the engine is, we will see the thermal efficiency is largely dependent on only the compression ratio.
Compression Ratio: The ratio between the maximum volume to the minimum volume in the cylinder i.e the volume when the piston is at bottom dead center(BDC) to the volume when the piston is at top dead center(TDC).
Fig 1: Cylinder at TDC & BDC
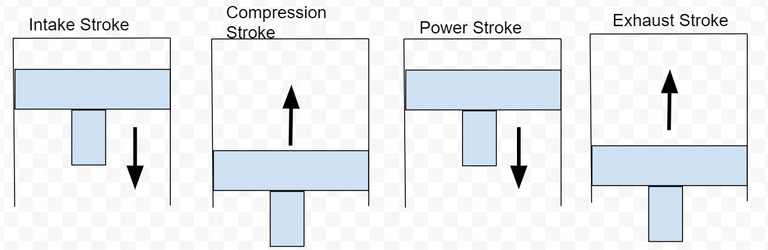
The four stroke Otto cycle
Engines have multiple cylinders. Each cylinder contains a piston bolted to the crankshaft that moves up and down as the crankshaft spins. If you have a vehicle and your vehicle has a RPM meter on the gauge cluster, you can see how fast your crankshaft is spinning. Typical gasoline engines can spin up to 6,000 revolutions per minute(RPM) if needed. To analyze thermal efficiency, we only need to investigate the engine block. No information from the cylinder head is needed, therefore I will not talk about any functions in the cylinder head. Complete engine construction can be for another post someday :). The cylinder head and the engine block are mechanically timed together. As the pistons move up and down, they are performing the Otto cycle. The Otto cycle has four strokes with one process occurring per stroke.
Process 1/Stroke 1: Intake stroke - piston moves down creating vacuum and air flow
Process 2/Stroke 2: Compression stroke - piston moves up compressing air
Process 3/Stroke 3: Power stroke - combustion forces piston down making power
Process 4/Stroke 4: Exhaust stroke - piston moves up to push exhaust gas out
Fig 2: Otto cycle
The ideal Otto cycle assumptions
Like many other machines, engines are incredibly difficult to model mathematically. In this post, we make assumptions to create the ideal Otto cycle.
- We assume exhaust process is replaced by a heat-out process that restores air
- We assume all processes are reversible (no losses)
- We assume no combustion instead there is heat-in from an external source
- We assume work is performed by air inside a closed cylinder and behave as an ideal gas
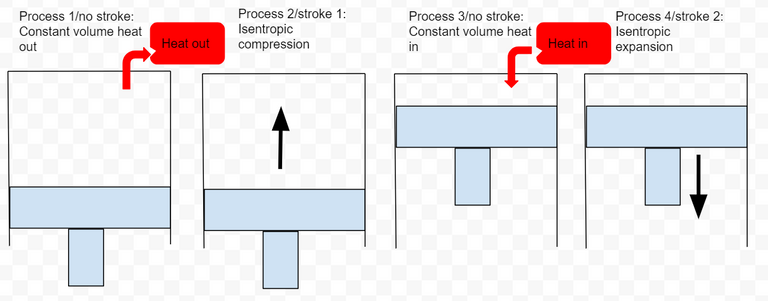
The ideal Otto cycle
Because of assumptions 1 & 3, we no longer have four strokes. Instead we have only two strokes but we still have four processes.
Process 1/nostroke: Base on assumption #1 we have constant volume heat out that restores the air (no piston movement)
Process 2/Stroke 1: Base on assumption #2 we have isentropic compression
Process 3/no stroke: Base on assumption #3 we have constant volume heat in(no piston movement)
Process 4/Stroke 2: Base on assumption #2, we have isentropic expansion
Fig 3: Ideal Otto cycle
Thermal Efficiency
At the simplest form, efficiency is the ratio of what you get out divide by what you put in.
where Wnet is the engine output(net work), and Qi is the heat in from process 3. Before we proceed, let's take a moment to talk about work and heat. Work and heat are both forms of energy transfer. Heat is the transfer of energy by a temperature difference, and work is the transfer of energy not by temperature e.g. mechanical transfer. There are other forms of energy transfer such as mass flow and electricity. However, for the ideal Otto cycle we can safely assume these to be 0. In addition, the ideal Otto cycle final state is the same as the initial state, resulting in the total change of energy to also be 0 i.e. the energy at the start is equal to the energy at the end. This ensures our simple model does not violate the first law of thermodynamics(energy cannot be created nor destroyed). If we do an energy balance, we find that our net work is equal to the difference between the heat-in and heat-out.
Total energy entering - Total energy leaving = Change in total energy
where
Qi = heat-in, Qo = heat-out, Wi = work-in, Wo = work-out. We can rewrite equation 3 as follows
Thus we can replace Wnet in equation 2 with the difference between Qi(process 3) and Qo(process 1).
To specifically analyze thermal efficiency, we break heat (Q) down further.
where m = mass, c = specific heat capacity, ΔT = change of temperature. Let's plug equation 6 back into 5 with respect to their processes.
Base on assumption #4, the mass and the specific heat of the air remains the same and will cancel out.
Base on assumption #2 we have isentropic processes, therefore we can apply the isentropic relationship between temperature and volume. Our isentropic processes are compression(process 2 to 3), and expansion(process 4 to 1).
And
where k = specific heat ratio, and T and V are the temperature and volume at their specific processes. Now let’s divide equation 9 by V4^k-1 to get T4 by itself, and also divide equation 10 by V3^k-1to get T3 by itself.
and
We are close to finishing. Do you see the V1/V4 and V2/V3 terms?
They are the compression ratio. You can confirm by looking at Fig 3, and check that V1 and V2 are at BDC, and V3 and V4 are at TDC. Now we just need to plug our isentropic equations into our efficiency equation, and do some algebra to make it look nice.
Recall our efficiency equation,
Now we plug in our isentropic equations into T3 and T4.
We know that the ratio V1/V4 = V2/V3 = compression ratio(CR). Let's rewrite equation 13 in terms of CR.
Now we factor out the CR.
Since T1-T2 is in both numerator and denominator, they will cancel out and we are left with
And that is it. That is our model for gasoline engine thermal efficiency using the ideal Otto cycle.
As you can see there are only two variables, the compression ratio(CR) and the specific heat ratio of air(k). Engineers do not have much control over k however, the compression ratio can be design into the engine. To get 100% efficiency, we need to make the 2nd term 0. That means CR needs to be infinity. Of course infinite CR is not possible, thus we can never have 100% efficiency. Well how high can CR be? Before we answer that, lets not forget about the k-1 term. k-1 is a power term in the denominator. This is very important to know because at some point, it will make efficiency have a diminishing return as you continue to increase CR. This requires engineers to find the optimal CR. In addition, gasoline engines have another critical limitation. If the compression ratio is too high, the pressure and temperature inside the cylinder will also be high resulting in detonation. Detonation is very bad, at least for gasoline engines. These factors have led gasoline engines to typically have a compression ratio around 10.
Fig 4: Compression ratio vs thermal efficiency(ignore the poor drawing at the start of graph)
Lets calculate the thermal efficiency of an engine with a compression ratio of 10. You can do a google search to get the k value for air. I got the value k=1.4 from engineeringtoolbox.com.
60% is very high efficiency. Typical gasoline engine efficiency will be below 40% with a CR of 10. Though this model does not predict efficiency accurately, it does tell engineers two things,
- The compression ratio is critical for efficiency
- At some point there will be diminishing returns as you continue to increase the compression ratio
Originally I was going to stop here, but I decided to not leave those of you who want to know actual efficiency hanging. For this, we can use experimental calculations with actual engine data. Let's go back to the original definition of efficiency - output divided by input. We can set output as engine power(horsepower), and input is our fuel power. Fuel power can be calculated with
where Mf is the mass flow rate of the fuel going into the engine, and LHV is the lower heating value of the fuel. Mf can be measure with sensors and equipment, and a typical LHV of unleaded gasoline is 44,500[kj/kg]. Therefore engine efficiency is
Lets go ahead and plug in some numbers. Say at 6,000[rpm] your engine makes 300[hp] or 225[kilowatt](if you use hp units, additional unit conversion will be needed), and the mass flow rate of the fuel at that instance is 0.02[kg/s]. Therefore,
25% is much more reasonable than our above calculation of 60%. The experimental calculation gives us more accurate efficiency values, but it does not tell us much information for designing the engine. Perhaps if I was an engineer, I would use the above theoretical calculation to design the engine, and then use the experimental calculation during testing. Of course engines are very complex, and there are a lot more parameters than just the CR to consider when designing an engine.
There you have it. The simple math behind engine efficiency. We had to apply some knowledge of thermodynamics, but I hope that was not too difficult to follow along.
Thanks for stopping by, and have a great day.
Greatness lies not in being strong, but in the right use of strength. -Henry W. Beecher
Sources:
Cengel, Yunus A, Boles, Michael A, Thermodynamics An Engineering Approach. New York: McGraw-Hill, 2011, Print.
Duffy, James A, Modern Automotive Technology. Illinois: The Goodheart-Wilcox Complany, INC, 2000, Print.
www.engineeringtoolbox.com



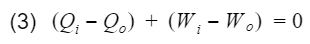
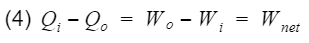
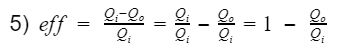
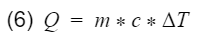

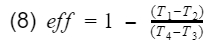
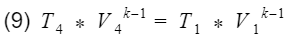
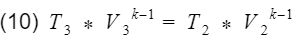
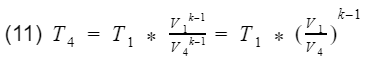
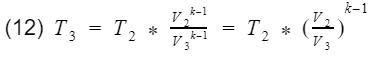

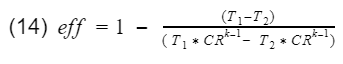
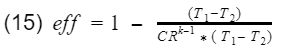


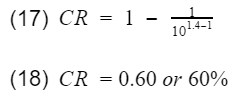
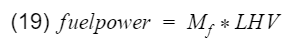


Congratulations @brokebook! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPCongratulations @brokebook! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOP