Simple Sorting

[devohier]

Hey, everyone!

I just wanted to share with you some stuff that I’m learning about in my data structures class right now. Specifically, some simple sorting algorithms!

An algorithm is a step-by-step process to go about solving a certain problem or performing a certain task. Usually there are many different solutions and algorithms available for simple problems, but one algorithm might clearly stand out as the best choice. Oftentimes the best option is the one that takes the least amount of steps (and resources). Here are 3 very popular and simple examples of sorting algorithms. That is, ways to go about putting an unordered array/list in order.

1) Bubble Sort:

Basic Steps:

1. Compare each item (except the last 1) with the item to the right of it.
2. If they are out of order, switch them.
3. Compare each element (except the last 2) with the item to the right of it. Swap them if necessary.
4. Compare each item (except the last 3) with the item to the right of it, swapping if necessary.
5. Continue until the list is sorted.

How it’s done:

Let’s say we have a small list, like this: [1, 9, 7, 4, 6, 8]
First we would compare 1 and 9. 1 < 9 so we would leave it as is. Next we examine 9 and 7. 9 > 7 so these need to be switched. Now our list looks like this: [1, 7, 9, 4, 6, 8]. Next up is 9 and 4, and we are going to switch these as well — [1, 7, 4, 9, 6, 8]. Then we will also swap the 9 with 6, and again with 8. At the end of this first cycle our list looks like this: [1, 7, 4, 6, 8, 9]. Notice that the largest number in the list is now in the last position. Now we know that we can leave the last position alone.

The whole process would look something like this:

This can be done using an outer for loop that decreases by one each run, keeping track of how many items in the list need to be checked each time (if n == number of items in the list, the outer loop will start at (n - 1), then (n - 2), (n - 3), and so on). An inner for loop goes through the list from left to right and compares its current item to the item directly after it. If the current item > the item right after it, they will be swapped.

Next up, selection sort!

2) Selection Sort

Basic steps:

(if the length of the list == n, so the last item in the list is in location (n-1))

1. Search the list from the first item to the last item → AKA: search items 0 - (n - 1)
2. Select the smallest one and switch it with the item in the first position of the list (location 0)
3. Search items 1 - (n - 1)
4. Select the smallest and switch it with the item in location 1
   5. Look through items 2 - (n - 1), select the smallest and switch it with the item in location 2
   6. Continue until there aren't any items left to search through

How it’s done:

Let’s say we are trying to sort this list [9, 1, 4, 6, 8, 3]
First we will look through the entire list. We will identify 1 as the smallest number and then put it in the first position of the list (position 0). The number that was in position 0 will be swapped for the 1, so we will put 9 in position 1. Then we will search the list again, but this time we do not even have to look at position 0 because we know that the smallest item is already there. We will identify the smallest item of the search, in this instance it is 3, and we will swap that with the item in position 1. Now we know that both position 0 and 1 are complete, and we do not have to look at these positions again. We will continue this process until the list is sorted and there are no more items for us to search through.

And last but not least, insertion sort!

3) Insertion Sort

Basic steps:

For each item in the list (other than the 1st one), find the 1st position to the left of the item that is <= (less than or equal) to the item. Then move everything to the right of that item over by one to the right and insert the item (directly to the right of the item that is <= to it).

How it’s done:

If we were to do this with the list [8, 4, 3, 2, 6, 9, 7, 1], we would begin by marking everything after the first item in the list (in this case, 8) as “unsorted.” everything to the right of the unsorted section (just the 8 right now) is “sorted.”
[8 | 4, 3, 2, 6, 9, 7, 1] Then we compare the first item of the unsorted section (4) to the item to the left of it (8). Since 4 < 8, we will swap them. Now we have [4, 8 | 3, 2, 6, 9, 7, 1]. We can now say that the first 2 positions are sorted, and now the unsorted section only contains the last 6 items.

This was just a short summary of some of the most basic sorting algorithms. There are many, many more, and some are much better than others. One very important thing to consider when dealing with large amount of data is how efficient the algorithm will be.

To demonstrate just the time difference between these 3 sorting options, one of my professors asked us to time how long it takes to sort 10,000 item arrays that are filled with random, ascending, or descending numbers using each algorithm. The time it takes would differ between computers, but here is how long each one took in seconds for my computer:

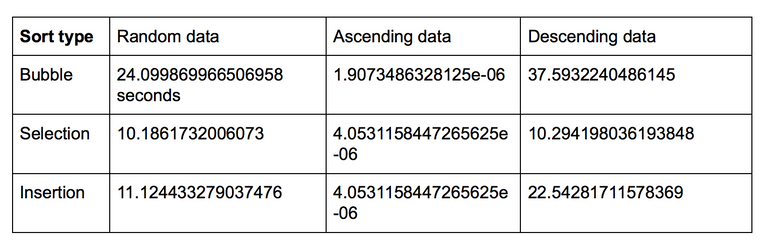
Bubble sort took by far the longest amount of time in each scenario. This sorting algorithm should really not be used with large amounts of data and I’ve been told that it’s safe to try and steer clear of it entirely.

Thanks for reading and I hope you learned a few new ways to sort a list today :)