Hello all my friends from the Steemit community, I was away for work reasons, now back I want to share with you a very simple mathematical technique known as square completions that help us solve equations such as:
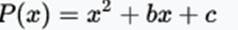
- Step 1
Adding and subtracting the quotient square (the division / fraction), the coefficient of x between 2
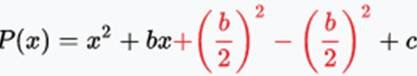
- Step 2
By grouping terms, you will get a perfect square trinomial. The terms x^2 , bx and + b^2/2^2
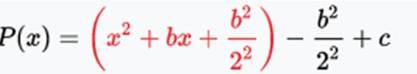
- Step 3
Factoring (reducing) this trinomial to a squared binomial, which was obtained: (1) extracting the square root of the first term from the trinomial sqrt(x^2) = x, which will be the left-hand side of the binomial; (2) by extracting the square root of the third term from the trinomial sqrt(b^2/2^2) = b/2, which will be the right term of the binomial; (3) using the sign of the second term of the trinomial + bx as the sign separating the terms of the new binomial
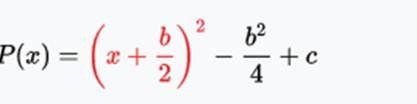
Here I leave an example of the application of this technique which is very useful when we just want to clear the variable and not find the roots of the quadratic function.
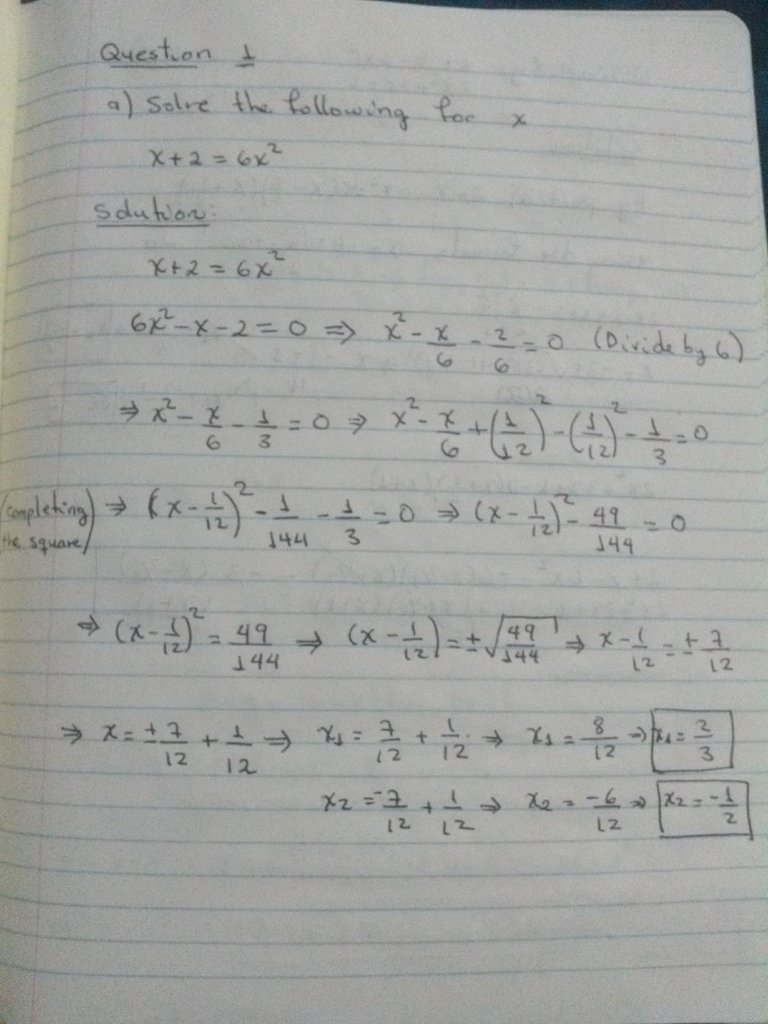
I hope you enjoy this technique, follow me @falcao12
Good to have you back falcao!
Never came across this method actually ^^ good little exercise to get my head around a the logic and usefulness of a new technique :)
Thanks for sharing!
thanks for your comment my friend
i like science and great post my friend
thanks my friend!!