Hello my friends, it is a pleasure to be here again, I want to show you some results that I obtained by doing internships in a meteorological station in my country Venezuela, the methodology uses stochastic differential equations and estimation by maximum likelihood to model precipitations of a locality and defines as follows:
A simple stochastic model for the rainfall at a certain location over a period of decades is developed. In this situation, a small time interval may be considered as one year. Let r(t) be the total rainfall at time t where r(0) = 0 for a starting time t = 0. Consider the possible changes in the total rainfall over a very small interval of time Δt. The possible changes in the rainfall for time interval Δt are assumed to be (Δr)1 = γ and (Δr)2 = 0 with probabilities p1 = λΔt and p2 = 1 − λΔt, respectively. Assuming these changes and probabilities, the mean change and the mean square change in the total rainfall are
Letting μ = γλ and σ =-γ2λ, the above expectations leads to the stochastic differential equation model for total rainfall r(t) of the form
dr(t) = μdt + σdW(t)
r(0) = 0.
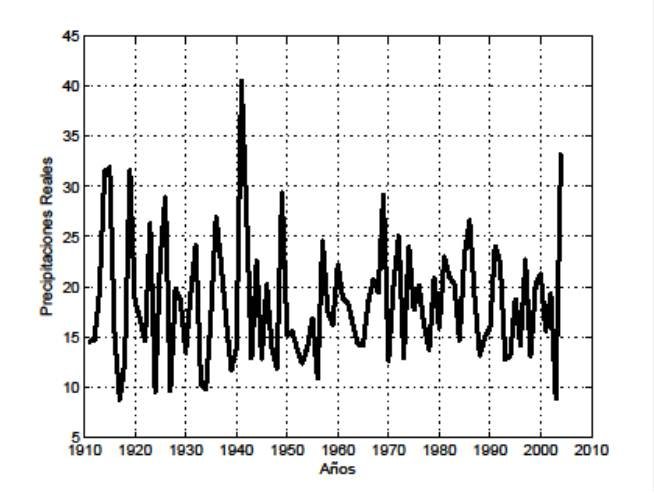
To test this model, the annual precipitation data for Lubbock, Texas was obtained from the National Weather Service and is plotted in Fig. 1. This data was fit to the stochastic differential equation model using a maximum likelihood estimation procedure. The values obtained for the parameters μ and σ were μ = 18.57 and σ = 6.11. Now consider the annual precipitation p.
r(t + Δt) − r(t) = μΔt + σ(W(t + Δt) −W(t)).
Letting Δt = 1, the annual precipitation for the ith year satisfies the model
pi = μ + σηi for i = 1, 2, . . . ,
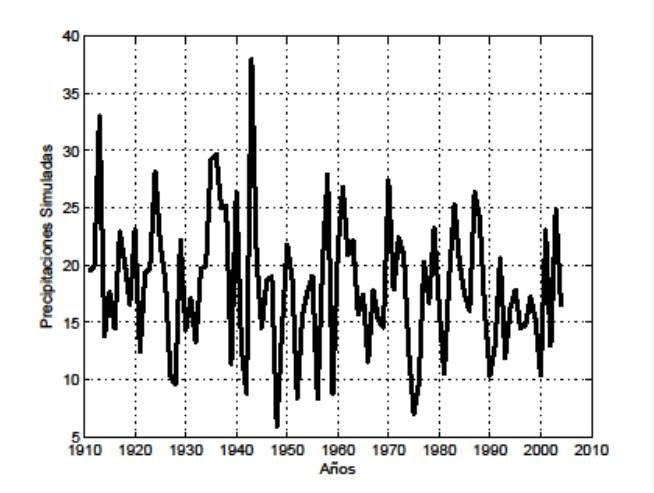
where ηi ∼ N(0, 1) for each i. A simulated precipitation using model is given in Fig. 2. The simulated yearly rainfall has a similar appearance to the actual yearly rainfall.
Enyoy, resteem, upvote and follow me @falcao12
W(t) is standard Brownian motion, correct? I somewhat remember some stuff from stochastic calculus.
That's right my brother is also known as Winer process
There's that alternate naming too, the Wiener process. Sometimes you see subscripts for the time variable t as in or you have the letter B as in B(t).
or you have the letter B as in B(t).
you are way beyond me man (-:
:) just it is my study area, my friend!! thanks!!
Upvoted and also resteemed!
thank my friend!!
Interesting
yes, very interesting my friend!!