Streeter Phelps Equation

[florencemaej]

Streeter Phelps Equation

Streeter-Phelps Model – DO sag curve

Many equations and computer programs are available today to describe the quality of water in streams, rivers and lakes
The most prevalent is the Streeter Phelps equation.
Addition of wastewater (BOD) typically causes a slow decrease in O2, followed by a gradual increase close to the dissolved oxygen saturation concentration (DOsat)

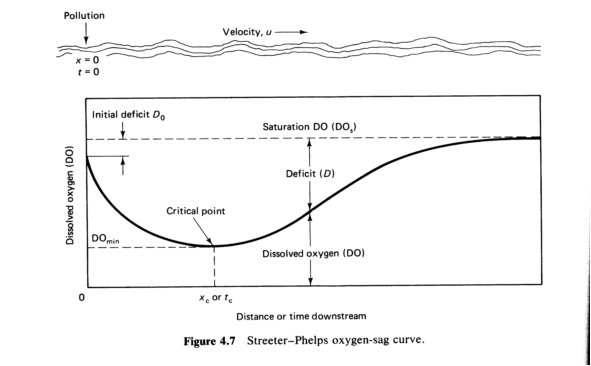
DO sag curve gives us the characteristic response in oxygen levels as a result of discharging oxygen-demanding wastes to a river or stream.
DO sag curve has 3 phases:
1. deoxygenation rate > reaeration rate
- DO levels fall
2. deoxygenation rate = reaeration rate
- Critical point
3. deoxygenation rate < reaeration rate
- DO levels increase, eventually reaching saturation
The critical point location and the DO level at this point are of principal interest because this is where water quality conditions are at their worst. Design calculations are based on this location.

Streeter-Phelps Model
Assumptions of the Model
stream is an ideal plug flow reactor
the only reactions of interest are BOD exertion and transfer of oxygen from air to water across air-water interface
Mass Balance for the Model
Not a Steady-state situation
rate O2 accumulation = rate O2 in – rate O2 out + O2 produced – O2 consumed
rate O2 accumulation = rate O2 in – 0 + 0 – rate O2 consumed
Both re-aeration and deoxygenation are 1st order rxns
rate of deoxygenation = -k1Lt
k1= deoxygenation constant, function of waste type and temperature

rate of re-aeration = k2D
D = deficit in DO or difference between saturation and current DO
k2 = re-aeration constant

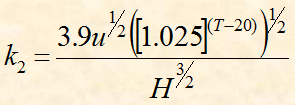
Where
T = temperature of water, ºC
H= average depth of flow, m
u = mean stream velocity, m/s
Oxygen Deficit
D = DOsat – DOact
DO deficit = saturation DO – DO actual in the water
Deoxygenation rate is equivalent to BOD of waste
ro = -k1 Lt or dL/dt = -k1Lt
Lt = Loe-k1t
Lo = ultimate BOD of the wastewater and stream water mixture
In terms of the deficit with time

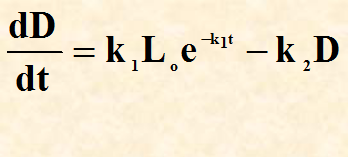
Source: Lectures notes from
Introduction to Wastewater Treatment
Lesson 8