Hello, Stemians! Today I want to add a new post to my blog in the new format - let me introduce [Thoughts] tag.
Let's go!

One day, I went to the shop and lost in my thoughts. I thought about how hard it can be sometimes to organise a party - someone always don't come! Hm, and what if we cancel party every time someone can't come. That's how this joke was born:
The joke
Okay, let's imagine the group of cool mathematicians who want to organise the Great Party. They want to choose the date ;-)
Lets also assume three things:
- All these guys are veery busy during the week and have only one holyday.
- All of them are pretty random and unexpected and this holyday can happen in every day of week.

- If someone have no holyday in the day of Great Party it will be cancelled!
So the main question is what is the expected value of waiting time?
In other words, how long the company of N mathematicians will be waiting before all holydays on a week will coincide?
That was the question that I ask to myself when think up such a situation :-)
So, after I came home I've decided to make this out!
Its easy to begin from two-case (N=2):
then expected value is :
probability to meet on the first week (1/7) multiplied on 1, plus
probability not to meet on the first and meet on the second week (1 - 1/7) * (1/7) multiplied by two, plus etc.
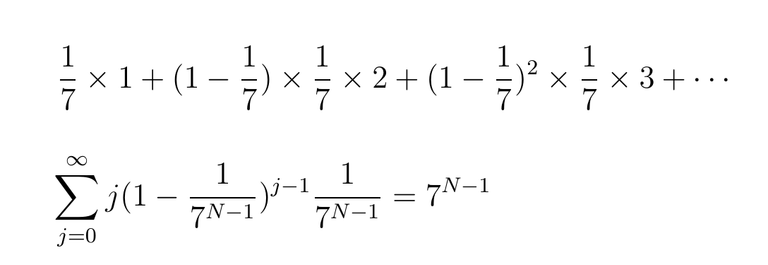
And when you solve it generally you finally get the answer: 7^(N-1) weeks on average!
So, it means that two friends should wait at least 7 weeks to meet on the party, three friends - 49 weeks (almost year).
And what about company of 10 awesome mathematicians?
Are you ready?
Five. Million. Years.

Conclusion
Such a funny result appeared because of strict conditions (only one random day of week and no party if someone can't go).
However it shows my irony about party organisation moments.
Thank you for your attention!
Comment your questions and ideas!
Follow my blog @ideamaker for more ;-)
I have to use this when trying to schedule a meeting with engineers! Mathematically proves how hard it is to get everyone in on the same meeting
I'm glad you appreciate it ;-)