"This is but an insignificant imitation of a much larger system whose laws you know, and I can not convince you that this simple toy has no designer or maker, however you affirm that the great original from which this design was taken has reached exist without designer or maker"
Isaac Newton: "The BRAQUISTÓCRONA"
THE BRAQUISTÓCRONA CURVE OF NEWTON
The fastest descent :
A brachistochronic curve is the curve that represents the shape of a ramp that is traveled in the shortest time possible by a body that starts at the starting point with zero speed and that must move along the ramp to reach the second point under the only action of a constant gravity and assuming that there is no friction.
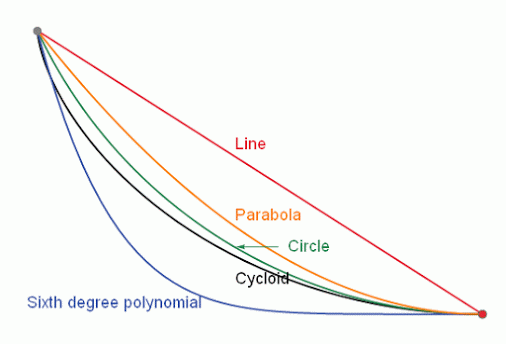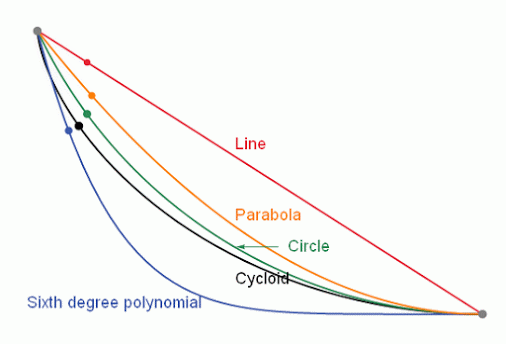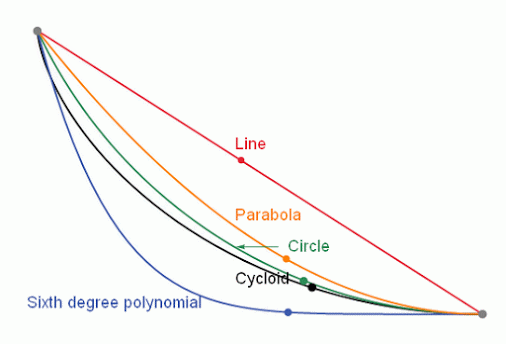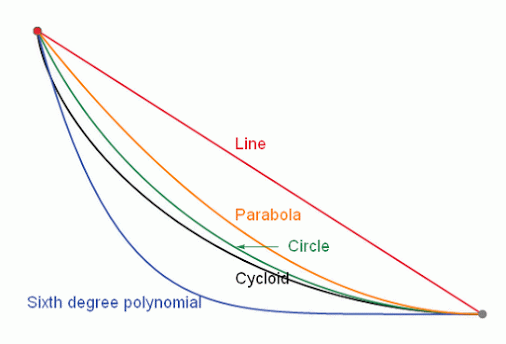
Intuition tells us that that ramp would have to have a straight line shape. This would make the distance between the two points the least possible but not that the descent lasted the shortest time.
In the attached animation the problem can be observed, where respective balls slide, respectively, through a straight line, a parabola, a circle, a cycloid and a sixth degree polynomial.
The correct answer is that the brachystochronic curve must be a cycloid curve.
Johann Bernoulli solved the problem in 1696, although several other mathematicians intervened in the solution, among them Leibniz, Newton or L'Hôpital. This was the first resolution with a new mathematical theory: the calculation of variations.
In addition, the cycloid is, also, a tautophore curve. That is, the time taken to reach the lowest point of a cycloid ramp by an object that slides without friction with uniform gravity is independent of its starting point. This is appreciated in this other animation: in its upper part appears the space-time graph for each object and the blue arrows represent the acceleration of each object.
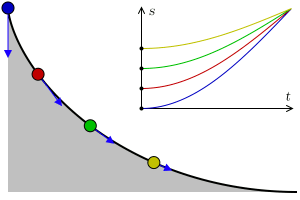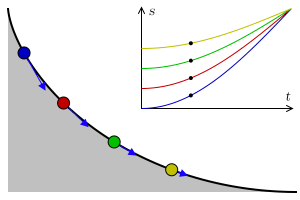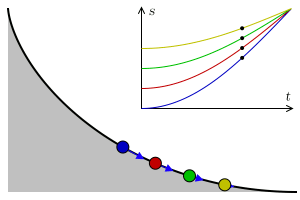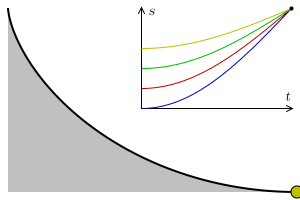
The brachistochronic is the cycloid
Given two points A and B, with A at an elevation greater than B, there is only one cycloid curve with the concavity facing up that passes through A with infinite slope (vertical direction and direction from top to bottom), also passing through B and not it has maximum points between A and B. This particular inverted cycloid is a brachistochronous curve. The curve does not depend on the mass of the body or the value of the gravitational constant.
The problem can be solved using the variational calculation algorithms.
If the body is given an initial velocity in A, or if the effect of friction is taken into account, the curve that minimizes the transit time will be different from the one described in the preceding paragraphs.
Demonstration of the brachychochronous exercise:
The conservation of energy requires that the vertical velocity of a body in a uniform gravitational field is given by:
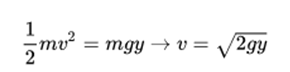
where y represents the vertical height from which the body has fallen. On the other hand, the space covered is given by:
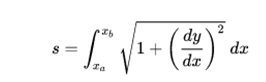
From the differential equation that gives the velocity it follows that the time between points a and b is given by:
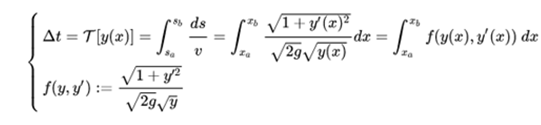
Since the curve that minimizes the previous functional satisfies the Euler-Lagrange equations, we have:
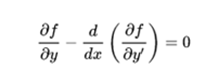
Since the function f does not explicitly depend on x the above equation is equivalent to:
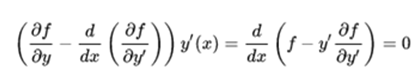
In other words, the solution to the problem of brachistochrome is a curve such that:
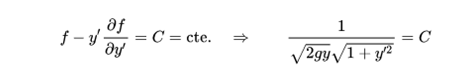
This equation can be rewritten as:
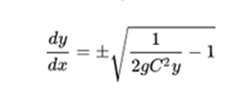
It can be seen that the cycloid curve defined parametrically as:
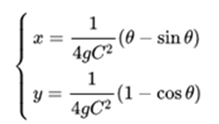
Satisfy the above equation with y (0) = 0, since:
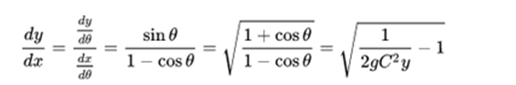
Properties
The brachistochronous curve also coincides with a tachycronous curve. A flat curve is said tautócrona if given a collection of material points that move along them that start at different points are at a point on the curve, ie they take the same time to reach a certain position.
Curiosities
According to the Fermat principle: The trajectory followed by a beam of light between two points is that which results in the shortest travel time. Therefore the brachistochronic curve would simply be the trajectory of a light beam where the light speed increases with a vertical acceleration (that of gravity)
As if this were not enough, this splendid video prepared by professors of the IES Historiador Chabàs de Dénia, Alicante, clarifies the concept even more:
Hello,
Regardless of our previous comments you you seem to keep copying and pasting content from the sources provided without adding anything original.
Copying/Pasting full texts without adding anything original is frowned upon by the community.
These are some tips on how to share content and add value:
Repeated copy/paste posts could be considered spam. Spam is discouraged by the community, and may result in action from the cheetah bot.
If you are actually the original author, please do reply to let us know!
More Info: Abuse Guide - 2017.
Mathematics is quite interesting especially when it comes down to its applications.
Thank you for the write up!