Find a square whose sides and diagonals are "counting numbers", i.e. 1, 2, 3, 4, ... to infinity.
The first one to comment with the counting number side length and counting number diagonal length of a square wins 10 SBD.
Like in the picture, if the length of the black lines of your square are counting numbers and if you are the first to post a correct answer in the comments here, you can win 10 SBD.
Bribe: All commentors that also upvote are rewarded so that everybody wins some SBD.

If you're mathophobic, it's ok.
Just think of math equations as beautiful art.
Maybe you can guess the answer. :)
The application of Pythagoras' Theorem is vitally important to art, math, physics, chemistry, home construction, engineering, and so much more.
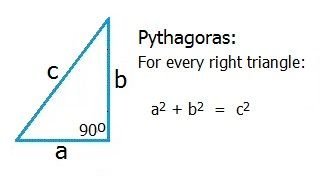
Pythagoras said that for all right triangles: a2 + b2 = c2
This works for all right triangles.
Try this:
If a = 3, b = 4, does c = 5 ?
Yes. 9 + 16 = 25
Thus 3, 4, 5 is always a right triangle
But the 3,4,5 triangle does not form the diagonal of a square.
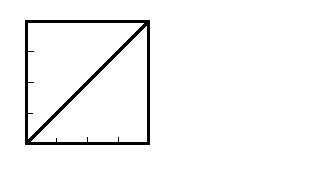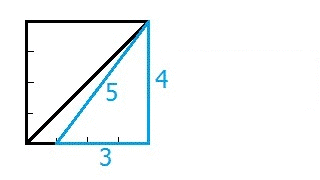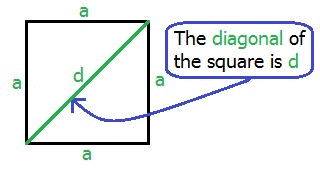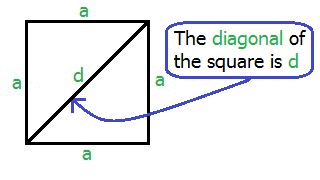
For a square a = b Now we have: a2 + a2 = d2

Sample comments (wrong answers):
a = 4, d = 6
(not a correct answer because 42 + 42 = 16 + 16 = 32 does not equal 62 = 36)
or
a = 1, d = square root of 2
(while true, it's not the right answer because the square root of 2 is not a counting number.)
My bribe to you:
All commentors that also upvote will be rewarded at least a part of an SBD.
Have fun with this little geometry art puzzle.
Its not possible to have a square whose sides and diagonals are countable numbers.
If 'a' is the side of square then from Pythagoras Theorem the diagonal is given by √2×a
As √2 is irrational and 'a' is a countable number and also we know that the product of a countable number and an irrational number is always an irrational number, hence the diagonal cannot be a countable number.
Hence, there is no possible square whose sides and diagonals are countable numbers.
Thank you for your reply
so it's impossible to win the 10sbd :-)
Haha, hope so😛😛
Don't know. Closest I came was a=7, d=10, but not quite.
Thank you for your reply