Introduction

Absolute zero can be defined as the temperature at which particles of matter are said to have no kinetic energy or have no motion at all. From Charles’ Law, a constant pressure system containing a constant amount of ideal gas, the volume of the gas is directly proportional to its temperature, that is

V = (nR/P) T = kT
where n is molar quantity, R is the universal gas constant, P is the absolute pressure, V is the volume, k is a constant, and T is the temperature in Kelvin.

_{Absolute Zero in Various Temperature Scales}

In statistical interpretation, raising the temperature increases the mean velocity of the gas molecules, and the rate with which they collide with the container walls increases, increasing the volume occupied by the gas. If the temperature decreased sufficiently to zero, the volume should ideally decrease to zero. This temperature is known as the absolute zero temperature equal to -273.15 C or 0 K.

Real gases, however, liquefy and solidify long before this theoretical limit. In fact, Third Law of Thermodynamics implies that absolute zero can only be approached but never be attained. Because of this, an experimental method has to be done in order to approximate its value. By using air as a sample of a real gas and limiting the temperature range, it is possible to estimate the absolute zero. By measuring volumes of air sample at diﬀerent temperatures, the temperature can be extrapolated to where the volume is zero, meaning the gas has no kinetic energy left. Since the volume of a gas cannot have a value less than zero, this is the minimum temperature value for all gases and all forms of matter in general, and this corresponds to what is known as the Absolute Zero.

Experimental

_{Experimental Setup}

A sample of air is trapped in a cylinder and was inverted into a beaker and then heated to about 85 ^oC. The system was cooled and twelve volume measurements of the gas was done in every certain temperature interval. Ice is added to the beaker until the temperature reaches zero. The volume is then recorded and plotted against the temperature which was extrapolated to zero volume to get the y-intercept which corresponds to absolute zero.

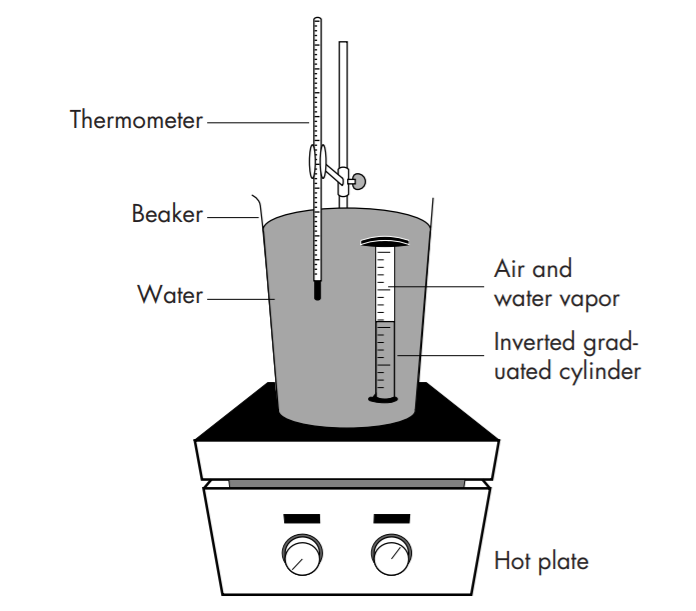
The partial pressure of dry air inside the cylinder is given by

P_air = P_total - P_H2O
Where Ptotal is equal to the barometric pressure and PH20 represents the vapor pressure of water at a specific temperature. The vapor pressure can be found through interpolation of steam tables found in handbooks. Alternatively, it can be calculated conveniently using the Antoine’s equation which provides a relationship between temperature and vapor pressure. This can be written as
log P=A+B/(C+T)
where A, B, and C are constants which varies for each substance and T is the temperature in Celsius. In the case of water vapor, A = 7.96681, B=1668.21, C=228 (Perry’s Chemical Engineering Handbook).
On the other hand, the partial volume of water vapor is

V_H2O=V_totalP_H2O/P_total

The partial volume of the air sample can be found by subtracting the partial volume of wate vapor from the total gas volume,

V_air=V_total-V_H2O = V_total(1-P_H2O/P_total)

Having calculated the Vair, a graph of Temperature and Volume can be generated, and the y-intercept can then be found by extrapolation to give absolute zero. The y-intercept can be obtained via linear regression.

Data and Calculations

Table 1. Temperature and Volumes of Water Vapor and Air

Temperature (^oC)	V_H2O(mL)	V_air(mL)
82.5	8.83	4.2725
75	6.75	4.185
67.5	5.64	4.0865
60	4.98	4.0022
52.5	4.53	3.9073
45	4.21	3.8128
37.5	3.98	3.7276
30	3.79	3.6322
22.5	3.64	3.5429
15	3.52	3.4615
7.5	3.40	3.3659
0.0	3.3	3.2806

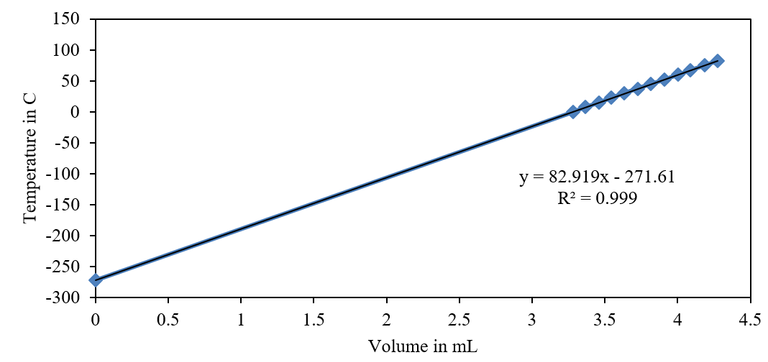
Figure 1. Plot of Temperature vs Air Volume

Table 2. Summary of Results

Experimental	Correlation	Theoretical	%error
-271.610^oC	99.99%	-273.15^oC	0.564%

Discussion of Results

As expected, the volume of air decreases with decreasing temperature which is in accordance to Kinetic Molecular Theory. Likewise, the vapor pressure of water also decreases with decreasing temperature due to lesser kinetic energy of water molecules resulting to lower rates of vaporization.

On the basis of R-squares which signified excellent linearity, it has been verified that indeed, volume varies linearly and is directly proportional with temperature as depicted by the Charles’ Law. The observed discrepancy between experimental and theoretical result is most likely due to the following reasons.

Tap water instead of distilled water was used in this experiment. Hence, the presence of impurities might affect the colligative properties of the system and might actually lower the vapor pressure of water which played a major role in the calculations.

In addition, the barometric pressure was not measured for each volume measurement but for each trial only. Hence, it was assumed that barometric pressure is uniform throughout each trial which does not hold true during abrupt atmospheric conditions which can cause sudden pressure rise or drop.

No corrections have been made to compensate the slight difference in water levels in the cylinder and the beaker. This might impose an error between the barometric pressure and the pressure inside the cylinder.

The humidity of air in the laboratory also affects the result. In this activity, it is essential that the air is substantially dry since at higher temperatures, the relationship between vapor pressure and temperature is not linear but a curve which contradicts the assumptions.

Lastly, air is not an ideal gas in the first place. It is actually a mixture of different gases. Also, the procedure was not carried out at a relatively high temperature and low pressure which are supposed to be the conditions for ideal gas equation to work well.

Image Sources

[1], [2],[3]

References

My Laboratory Experiments
Atkins P.W., de Paula J., Physical Chemistry, 8th Edition, Oxford University Press
Kim M., Song Kim M., Ly, S Lab Experiments, J. Chem. Ed., 2001, 78, Vol. 2.

Determination of Absolute Zero Temperature