Bevor wir uns nun an die Dimensionsbegriffe und Dimensionen der Fraktale machen wollen wir zunächst erst ein Verständnis für den klassichen Dimensionsbegriff bzw. die klassischen Dimensionsbegriffe erhalten.

In der Elementargeometrie ist zunächst klar:
Eine Punkt ist nulldimensional.
Eine Strecke ist eindimensional mit der Länge: 0 <𝐿(𝐴) <∞.
Ein Flächenstück ist zweidimenisonal mit dem Flächeninhalt: 0 <𝐹(𝐴) <∞
Ein Körper ist dreidimensional mit dem Volumen: 0 <𝑉(𝐴) <∞
Die Maße werden oft einfach unter dem Begriff n-dimenionales Volumen zusammengefasst.
Wenn wir es nicht mehr mit den einfachsten geometrischen Objekten zu tun haben wird das ganze schon etwas schwerer, welche Dimension hat beispielsweise folgende Kurve?

Intuitiv würden ihr die meisten wohl die Dimension dim(X)=1 zuordnen.
Manche werden zurecht aber anführen, dass man eine Fläche benötigt um die Kurve darzustellen
und ihr somit die Dimension dim(X)=2 zuordnen. Beide haben sie nicht ganz unrecht,
je nachdem nach welchem Dimensionsbegriff man ihr die Dimension zuordnet.
Topologische Dimension
Sie entspricht meist der „intuitiven“ Dimension, jedenfalls wenn man bei der oben genannten Kurve dieser intuitiv die Dimension dim(X)=1 zugeordnet hätte.
Vereinfacht erklärt bestimmt man hier die Dimension der einfachsten topologischen Transformation des Objekts.
In der Topologie gibt es gewisse "Verzerrungsregeln" die wichtigsten und einfachsten, mit denen wir uns hier begnügen wollen sind folgende:
- Löcher/Verbindungen dürfen nicht übereinander hinwegbewegt werden
- Löcher/Verbindungen dürfen nicht verschwinden
Damit lässt sich bspw. eine Kurve zur Strecke umformen, eine Tasse zum Donut oder ein Zylinder zum Kubus transformieren.
Solche Objekte nennt man auch zueinander homöomorph, d.h. topologisch identisch.
Eine exakte mathematische Festlegung dieses Dimensionsbegriffs erhält man
über die Lebesque'sche Überdeckungsdimension
Diese wurde nach dem franz. Mathematiker Henri Léon Lebesgue (1875-1941) bennant.
n gibt hierbei dei Überschneidungszahl
(d.h. die Zahl mit der Kugeln mit der sich jede Kugel maximal überschneidet)
an und Ziel ist es das Objekt mit kleinen Kugeln/Kreisen so zu überdecken, dass n minimal wird.
Die Dimension lässt sich dann berechnen mit folgender Formel:
dim(X)=n-1
Einbettende Dimension
Wie der Name es schon sagt gibt diese an, in welche Dimension das Objekt einbettbar ist.
Am Besten lässt sich diese Dimenision mit der Beantwortung
einer der folgenden äquivalenten Fragen bestimmen:
In welchen Vektorraum ℝ^𝑛 (𝑛 minimal) ist das Objekt einbettbar?
Ab welchem Vektorraum ist das Objekt darstellbar?
Wie viele linearunabhängige Vektoren sind nötig um jeden Punkt zu erreichen?
Wie oben schon angerissen und in Fraktale - Großbritanniens Küstenlinie bemerkt reicht diese Dimensionsbegriffe nur in der klassischen Geometrie und nicht in der fraktalen Geometrie aus.
Das Problem wird deutlich an den Cesàro-Kurven 1905
von Ernesto Cesàro (ital. Mathematiker 1859-1906)
als Veralgemeinerung der Koch-Kurve (60°) "eingeführt".
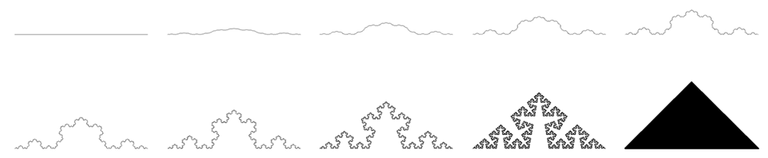
Cesàro-Kurven von 0° bis 90° die Konstruktion geht nach dem gleichen Prinzip wie das in Fraktale - Mathematische Monster erklärte der Koch-Kurve.
Alle besitzen sie die topologische Dimension, der Dimension von der man meistens in der klassischen Geometrie ausgeht, dim(X)=1 schaut man sich die Kurve für höher werdende Gradzahlen an scheinen diese immer weniger eindimensional zu sein, bis sie für 90° kein bisschen eindimensional aussieht und an ein Dreieck erinnert und somit die Dimension dim(X)=2 haben müsste. Irgendwie müsste also ein Dimensionsbegriff erschaffen werden, der nicht nur die Natürlichen Zahlen verwendet sondern auch die Reelen zulässt um den Übergang von eindimensional zu zweidimensional zu beschreiben.
Mathematisch lässt sich diese Notwendigkeit noch anders Begründen.
Auf Grund ihrer Konstruktionsweise ist die Koch-Kurve eine Kurve, die überall stetig ist, aber niergends differenzierbar d.h. eine Kurve ohne Tangente.
Oben haben wir für die Elementargeometrie definiert:
Eine Strecke ist eindimensional mit der Länge: 0 <𝐿(𝐴) <∞.
Ein Flächenstück ist zweidimenisonal mit dem Flächeninhalt: 0 <𝐹(𝐴) <∞
Für die Kochkurve ergibt sich nun:
Länge: 𝐿(𝐴)=∞
Flächeninhalt: 𝐹(𝐴)=0
Für die Kurve muss somit 1 <𝐷 <2 gelten.
Die verschiedenen Dimensionsbegriffe die in der fraktalen Geometrie anwendung finden werden wir uns das nächste Mal genauer anschauen.