Wie lang ist die Küstenlinie Großbritanniens?
Dieser Frage, wird sich die heutige Ausgabe der Reihe "Fraktale und Chaostheorie" widmen.
Ebenso soll dies als Aufhänger für die nachfolgende Unterthematik der Dimenisonen dienen.

1967 stellte Benôit B. Mandelbrot (franz.-amer. Mathematiker 1924-2010)
eben diese Frage in der Zeitschrift science.
Diese Frage klingt zunächst ziemlich trivial, man nehme einfach ein Linial,
messe auf der Karte nach und rechne das ganze maßstabsgetreu um.
Alternativ könnte man das ganze ja auch mit einem Meterstab oder einem Geodreieck abmessen.
Problem: Je kleiner man die Maßeinheit wählt desto länger scheint die Küste zu werden,
da man in immer mehr Einbuchtungen gelangt.
Statt Maßeinheit wird hier meist das Wort "Auflösung" verwendet.
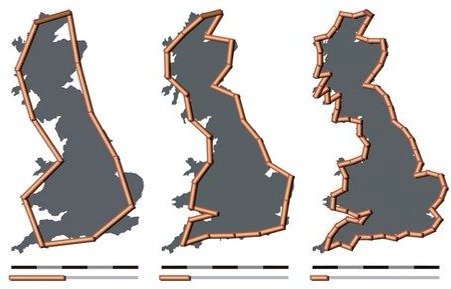
Wenn man nun das Limit (den Limes) der Länge wissen will
und somit das Maßband immer kleiner werden lässt,
so strebt die Länge gegen unendlich, irgendwann stößt man auf Atome und misst entlang dieser.
Nun haben wir die Küste zwar als unendlich lang vermessen,
können diesen Wert jedoch nicht sinnvoll gebrauchen.
Jede natürliche Küstenlinie hätte so die Länge unendlich,
Küstenlinien wären bezüglich ihrer Länge nicht mehr unterscheidbar.
Großbritanniens Küstenlinie etwa so lang wie Skandinaviens.
In der Praxis wird dieses Problem gelößt, indem man eine Auflösung festlegt und alle Küstenlinien mit der selben vermisst, etwas mit einem Maßband von einem Meter Länge.
Perfektionistisch wie Mathematiker sind geben sie sich jedoch damit nicht zufrieden
und wollen ein exaktes Maß, das Küstenlinien vergleichbar macht.
Wenn schon nicht hinsichtlich ihrer Länge, dann muss etwas anderes herhalten.
Zur Hilfe kam hier die Hausdorff Dimension von Felix Hausdorff (dt. Mathematiker 1868-1942)
aus dem Jahre 1918.
Mit ihrer Hilfe wurde Englands Westküste ein Wert von ungefähr 1.21 zugeordnet.
Alles weiter zum Thema Dimensionen folgt in den nächsten Artikeln.
Die Frage ist eher, welches Maß ist Sinnvoll. Daran erkennt man vor allem die Tatsache, dass in der Natur absolut nichts so ist wie in der Mathematik, weil alles in einem Kontext stattfindet.
Mathematik hat aber auch nie den Anspruch erhoben die Natur abzubilden. Leider vergessen das schlecht gebildete Mathematiker nur all zu gern und suchen nach Lösungen die keinen Nutzen und keinen Realitätsbezug haben und auch keine Lösung bieten.
Wenn man sich die klassische Geometrie im Vergleich zur fraktalen Geometrie anschaut, dann merkt man dass sie sehr schlecht geeignet ist die Natur darzustellen. Wenn man nach draußen schaut und sieht eine Kugel, ein Dreieck, ein Kreis oder eine Linie, dann ist es sehr wahrscheinlich, dass diese Form vom Menschen geschaffen wurde und nicht natürlichen Ursprungs ist. Es ist stark vereinfacht und idealisiert. Fraktale sind aber auch meist, wenn es nicht nicht um natürliche Fraktale wie Küstenlinien handelt stark idealisiert, jedoch in die andere Richtung. Die Natur hat eine Balance zwischen einfach, glatt und komplex, gebrochen gefunden.