
Nach 7 Tagen nun endlich die Fortsetzung der fraktalen Dimensionen.
Wie schon im ersten Teil festgestellt gibt es Objekte bei denen es nicht möglich ist diesen über die Ähnlichkeitsdimension einen Wert für die fraktale Dimension zuzuordnen.
Man hat jedoch festgestellt, dass wenn man Objekte der Elementargeometrie mit einem Gitter überdeckt und dieses immer feiner werden lässt sich der Logarithmus der Anteil der Kästchen in denen sich Teile des Objekts finden durch den Logarithmus der Maschenweite geteilt wenn man nun die Maschenweite gegen 0 gehen lässt die Dimension ergibt.
Diese Art die fraktale Dimension zu bestimmen nennt man
Box-Dimension
Zur Bestimmung der selben überdeckt man das Objekt also mit einem Gitter der Maschenweite ε, zählt nun die ausgefüllten Kästchen Nε und erechnet mit Hilfe der Formel:
dim(X)=lim(𝜀→0)log(𝑁𝜀)/log(1/𝜀)=lim(𝜀→0)log(𝑁𝜀)/log(𝜀)
Das Gitter muss nicht zwingend zweidimensional sein, so kann man Kurven bspw. auch abzirkeln oder mit einem Maßband vermessen.
Hier ergibt sich jedoch wieder das Auflösungsproblem, dass wir schon in Fraktale III - Großbritanniens Küstenline bemerkten.
Für Objekte wie die Mandelbrot Menge, die ich in einem späteren Post einmal behandeln möchte genügt die Boxdimension völlig. Aber die Dimension der Küstenlinie lässt sich dennoch nicht bestimmen, da irgendwann, wenn man atomare Maschenweitengröße hinter sich gelassen hat, man als Ergebnis dim(X)=0 erhält.
Deshalb entwickelte man, durch kleine Abänderung der Box-Dimension die
Dimension natürlicher Fraktale
Dabei plottet man einfach 𝑁𝜀 und 𝜀 und erhält eine Trendlinie der Form 𝑓(𝑥)=𝑐𝑥^𝐷
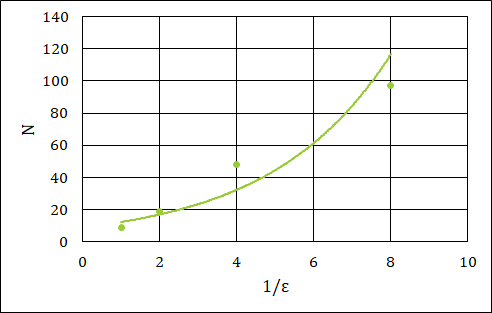
Hier mal beispielhaft für die Küstenlinie Großbritanniens mit einer Trendlinie 𝑁≈9,5∙(1/𝜀)^1,21.
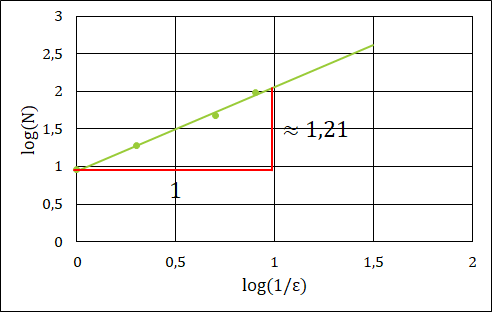
Zum einfacheren Ablesen verwendet man oft einen Doppellogarithmischen Plot (Log-Log-Plot), bei dem die Achsen logarithmisch anwachsen.
D.h. eine Trendlinie der Form log𝑓(𝑥)=log(𝑐𝑥^𝐷)=log(𝑐)+𝐷log(𝑥)
und im Falle der Küstenlinie die Trendlinie log(𝑁)≈log(9,5)+1,21log(1/𝜀)
Die Festlegung der fraktalen Dimension, die am meist verwendetsten und komplexesten ist ist jedoch die Hausdorff-Besicovitch-Dimension, welche ich möglicherweise irgendwann später als Nachtrag zu den Dimensionen behandeln werde.
Für die einzelnen Dimensionen gilt, sofern definiert:
einbettende D≥Box-D≥Ähnlichkeitsd.=Hausdorff-D.≥Topologische Dimension.