
Für alle, die sich in den letzten Posts der Reihe gefragt haben, was denn nun endlich diese Fraktale sind hier die Auflösung!
Das Wort Fraktal kommt aus dem lateinischen und heißt so viel wie zerbrochen.
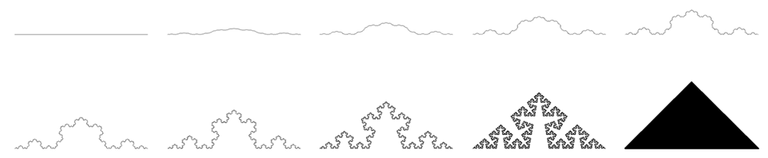
Mit Hilfe der fraktalen Dimensionen haben wir nun eine Möglichkeit gefunden die Komplexität bzw. Gebrochenheit von Fraktalen zu beschreiben. Mit steigendem Winkel der Cesàro-Kurve steigt auch die Komplexität der Kurve, wie oben sehr schön zu sehen ist.
Definiert ist ein Fraktal nun als ein Objekt derren Hausdorff-Dimension (Post dazu folgt unter Umständen noch) größer als derren Lebegu'sche Überdeckungsdimension, wie in Fraktale IV - Dimensionen in der klassischen Geometrie erklärt, ist.
Die Lebegue'sche Überdeckungsdimension kann der Einfachheit halber durch die topologische Dimension ersetzt werden, ein paar wenige Objekte werden dadurch jedoch unter Umständen falsch zugeordnet.
Am schnellsten lässt sich erkennen, wenn die Hausdorff-Dimension nicht ganzzahlig ist. Auch in diesem Fall handelt es sich definitv um ein Fraktal.
Natürliche Beispiele für Fraktale wären:
Farne, Romanesko, Biltz, Bäume, Küstenlinien uvm.

Ein besonders interesantes Fraktal ist die Drachenkuve.
Numberphile