In this post I'll explain how your computer can grow nicely looking trees and plants. Surprisingly, there will be turtle involved...

I am a fan of self-organizing systems and complexity that can emerge from simple rules. Today I want to tell you about such a very simple system that can draw beautiful plant like structures. In the late sixties the Hungarian biologist Aristid Lindenmayer developed so called L-Systems (yes, L stands for his last name), a formal grammar to simulate plant growth and development.
What is so special and fascinating about these L-Systems? Well, first of all, the underlying principles are relatively straightforward, yet they can yield very complex behavior; I'll give you some examples below, bear with me for a second, though. Secondly, even the mathematically notation of these systems is easy to understand (I swear, do not run or panic because I said math :-D).
The Basics of L-Systems: Meet the happy Turtle!
Basically, L-Systems are generative grammars, that is a set of rewriting rules for characters and strings. I'll skip the formal definition, but like to show an example instead. Consider the following two rules:
A -> ABA
B -> A
The arrow can be interpreted as replace the stuff on the left hand side with the other stuff on the right. In this example the character A will be replaced by the string ABA and B simply by A. It is important that both rules are applied simultaneously and not one after the other. In addition, we can repeat the string replacements as often as we want.
Let's say we start with character A. After the first iteration A will be replaced by
ABA. The second rule B -> A cannot be applied, because B does not exist, yet. Next, a second application of the rule set to ABA will yield ABAAABA (replacing both As by ABA and the single B by A). We could go on for a third, fourth or fifth time, as often as it pleases you.
Well, this nice rule set allows us to generate exponentially growing strings. Still, this does not really look like plant growth. A first step in this direction are the famous turtle drawings. Older generations may remember them from the educational programming language LOGO.

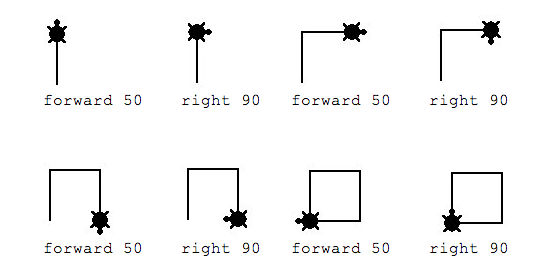
Imagine a turtle living on a paper plane. Moreover, someone very mean put a pencil right through the poor animal. However, the turtle doesn't die from the gruesome deed of being stabbed with a pencil. Instead, if the turtle wanders across the paper plane, it will draw a line along its path on the ground. It's also a very obedient turtle, it will walk in any direction you command it to. In fact, the turtle knows three commands F for moving a fixed length forward, + for turning left with a fixed angle, and - for turning right into the opposite direction. See below for a turtle with a turning angle of 90 degrees. See how happily it draws the cube?
Now we can use our set of symbols F, +, and - in combination with an L-Systems grammar to draw beautiful structures. For example, let's take a look at this very simple rule:
F -> F+F--F+F
With this we can generate the following strings iteratively:
We begin with F, then we get F+F--F+F (1st iteration), next F+F--F+F+F+F--F+F--F+F--F+F+F+F--F+F (2nd iteration), and so on.
We may stop at some iteration of our choice and let our turtle draw the resulting string
using an angle of 60 degrees for + (left) and - (right). Our turtle will read the string character by character and draw for us. For instance, let us take F+F--F+F, in this case the turtle will start to move forward, then turn left, forward, right twice, forward again, left and another last time forward. The resulting fractal graphs are called Koch curves:
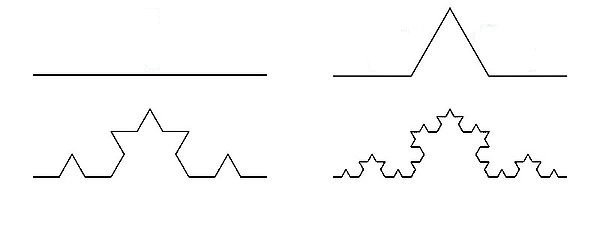
You see the initial start Fon the top left, followed by the first application F+F--F+F on the top right, and so on.
We can draw some slightly more complex structures. If we tell the turtle to also move forward not only for the letter F but also for G, we may feed it the following grammar:
F -> F-G+F+G-F
G -> GG
Starting with the string F-G-G and using a turning angle of 120 degrees, the turtle can draw so called Sierpinski triangles:
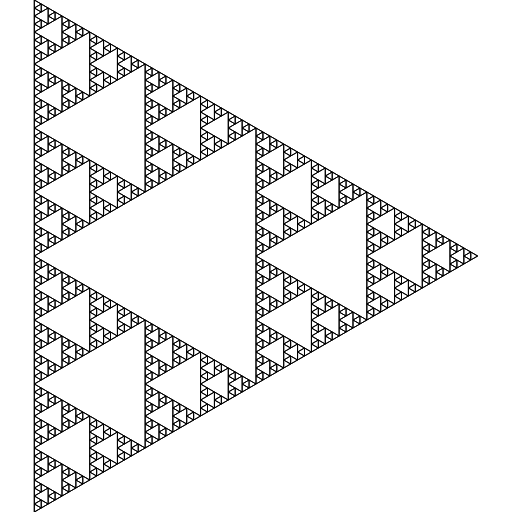
Beautiful Trees and Plants in Part 2, Pinky Promise!
Before turning our turtle into the perfect gardener, let us take a break here. But I promise, we'll get to beautiful plants in the next part! If you cannot wait and want to play around with L-Systems yourself, I provided a little Python script to do so on my Github profile.
Part 2
You can find part 2 now HERE!
This post has received a 0.28 % upvote from @booster thanks to: @smcaterpillar.
Hmmmm.....interesting, where did ju get this news?
Thanks, I had some lectures on L-Systems during my studies. There will be explicit references to papers in part 2 for those who are interested in a deeper dive.
STEEM WitnessYou got a 0.42% upvote from @upme requested by: @smcaterpillar. Send at least 2.5 SBD to @upme with a post link in the memo field to receive upvote next round. To support our activity, please vote for my master @suggeelson, as a
PART 2 is now published!
@originalworks
Ow! I wanted to grow a real plant :'(
Ah, ok maybe this doesn't really help then :-D
At least you could try to simulate how your plant is going to look like while you wait for the seeds to sprout.