The Rolle’s theorem! This is one of the core theorems in calculus and it is one of the easier concepts to grasp, but what does it say and why do is it one of the coolest theorems out there?
In more Mathematical terms if a function is:
Differentiable on the interval excluding the points A and B
If the output value of the function at point A = the output value of the function on point B
Then there exist at least one point C an element of the interval A and B such that the derivative of the function on point C is equal to 0.
Here is a sketch that explains visually what it means.

This might seem intimidating to the casual reader but here is the simpler explanation:
- If you have a smooth continuous line
- The endpoints are on the same horizontal line
Then there is at least one point between the two end points such that if you could put a level instrument on that point, you will see it is horizontal.
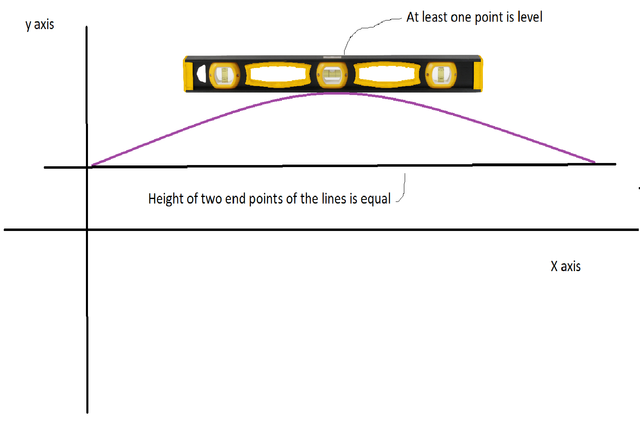
Intuitively it makes sense, here is a little experiment that you could do at home with a level instrument:
Try putting it on a flat table (preferably a level one) or try playing it by shifting the heights of the two end points.

Notice how close the instrument indicates a level position when the two end points gets closer and closer to each other's height.
You get the same result with an instrument that has a curved bow like this:
So clearly we knew this for hundreds of years, but only recently in human history did we find a mathematical proof of this concept. This is like I mentioned a core theorem and quite an easy proof. It is important to note that it was easy to prove, mathematically, for a straight line but it was not possible to proof for any curves without calculus!
How does one prove the theorem?
Okay so the proof starts of with three basic cases and we argue our cases by using the extreme value theorem and Fermat's theorem (I will cover these theorems in a later post, let me know in the comments if you want to read about it) I will explain these theorems and you will just have to assume it is true for all functions that satisfy the following scenarios:
Continuous on a certain interval A and B
Differentiable on the interval excluding the points A and B
Now let us start the proof by assuming the following properties for all three cases:
Continuous on a certain interval A and B
Differentiable on the interval excluding the points A and B
The output value of the function at point A = the output value of the function on point B
Ok case 1: a straight line.
if bothe values f(A) = f(B) then f is a constant.
Thus f(x) = K
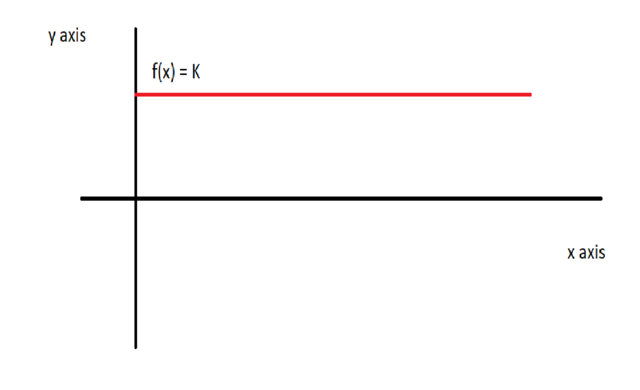
We know from derivative properties in calculus that the slope of a constant function is equal to 0.
Please note the [] brackets means that C can be any value of the interval A and B including the values of A and B. and the E means “element of”. Thus, it means it is part of the interval. F’ means the derivative of the function f.
Thus, for our case:
For any C E [A,B], f’(C) = 0;
Thus case 1 is proven.
Please note the () brackets means on the interval A and B but it excludes the points A and B. basically it means x can be any value except A and value B.
Case 2: f(x) > f(A) for some X E (A,B)
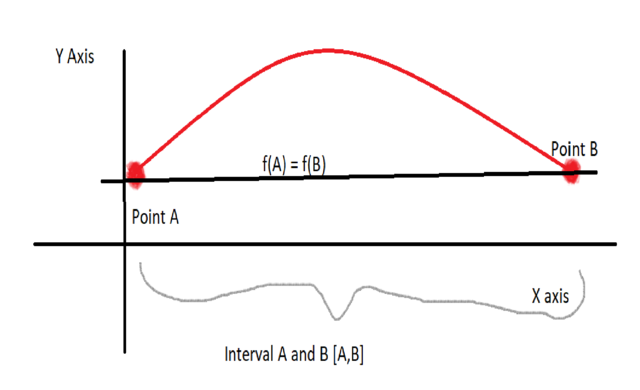
The Extreme Value theorem states that if a function satisfies the scenarios mentioned above, then a function must have at least one absolute maximum or absolute minimum the interval [A,B]
Thus in our case since any value of x is greater than any value of f(A) and we know f(A) = f(B) , so there must be an absolute maximum. AKA a peak that is the highest point on the interval. So we know the following there is a point C E (A,B) such that f(C) is has the highest value on the graph.
Now Fermat’s theorem comes into play. It states the following, if a function satisfies the statements mentioned above then the absolute maximum/ minimum point’s slope = 0.
Thus, we know that the point C which we know exists also has the property such that f’(C) = 0;
Thus case 2 is proven.
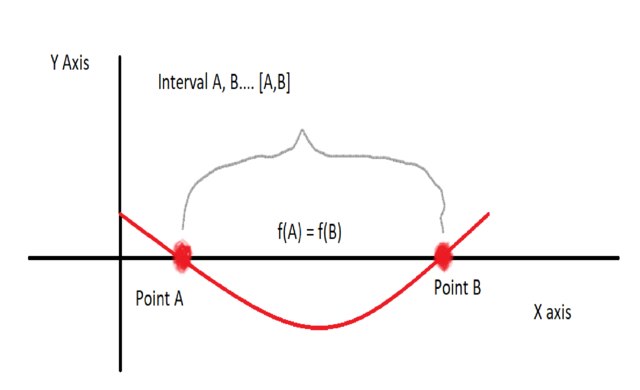
The same logic applies for the third Case is for a function f such that f(x) < f(A) for some X E (A,B) .
I like Rolle’s Theorem because it is a classic example of a mathematical proof that could be used to explain the reality of our world! Should I do more proofs? Let me know in the comments down below!
As always thanks for reading!
what do you think? leave a comment down below. Do not forget to upvote, Resteem and follow my blogspot!
check out more posts Here
Please Resteem It would really help my blog!



Great post
followed , upvoted
Thank you for the reply and follow!
You're welcome
Can you check out my blog ?
Yes, I am eager to look at yours!
Thanks
Nice post
Thank you for the reply!
Congratulations @stormblaze! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honnor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPBy upvoting this notification, you can help all Steemit users. Learn how here!
Interesting post