
Hello everyone! Have you missed DCS? Today we are going to talk about one of if not THE most famous unsolved problem in computer science. It's called "The P versus NP problem" and it's been around for many years.
In DCS #2 we learned about algorithms and that they are nothing but sequences of steps to perform tasks. But it turns out that not all tasks are as easy to solve!
The P versus NP problem consists of proving or disproving that all algorithms that are easy to check are also easy to compute. These algorithms are in special sets called P and NP. Let's take a look at what that means:
The lovely P problems
In computer science you can't measure an algorithm complexity by measuring time. After all, a faster computer can perform the same task in less time. So scientists measure complexity in a much clever way: by counting how many important operations a computer would need to execute in order to perform the algorithm.
Imagine that you and your friends are sitting in a restaurant table having a lovely dinner but it's time for you to go home. You definitely don't want to be rude so, before you leave, you say goodbye to every friend on the table.

Photo by Kevin Curtis on Unsplash
If we treat this scenario as an algorithm to leave the table you have to consider that the most important and time-consuming operation in this case would be saying goodbye to a friend. If we have 2 friends, we'll talk to 2 people, if we have 10 friends, we'll talk to 10 people, if we have N friends, we'll talk to N people!
We can clearly see that this algorithm's complexity is proportional to the number of people we have on the table, so we say that this algorithm has a complexity of N. Since this is the simplest way of saying goodbye to everyone individually it means that the problem as a whole has a complexity of N.
That same way there are problems with complexities N2, N3, N10, etc. A N3 problem is harder to solve then a N2 because the more N grows, N3 will require much more operations than N2. We call these "polynomial problems" (or P problems for short) because their difficulty is modeled by polynomials (remember that from school?) and we consider they the "easy" problems to solve (although it's not really like that!) because their difficulty curve grows much slower than problems with complexity functions like N!, 2N, NN for instance. Don't believe me? Let's plug in some numbers to have an idea:
| Complexity Function | N=2 | N=5 | N=10 | N=20 |
|---|---|---|---|---|
| N2 | 4 | 25 | 100 | 400 |
| N3 | 8 | 125 | 1000 | 8000 |
| N! | 2 | 120 | 3628800 | 2432902008176640000 |
| NN | 4 | 3125 | 10000000000 | 104857600000000000000000000 |
Wow, that escalated quickly! Look at how many operations!
NP Problems and the big question
Right now, there is a bunch of problems to which the only solutions we know are very complex and hard to compute. But some of these problems can have their solutions verified easily in polynomial time. These problems are called "NP problems".
Here's what I mean: let's say you have N random people and you want to know if there is any way you can sum the ages of a few of those N people to obtain the number 1337. That involves trying out different combinations and doing clever things to find the answer but the solution, once you have it, is fairly easy to check if it's correct. You only need to sum up the ages of the selected people to see if it's 1337 and you're done!
What scientists realized is that all P problems have easy-to-check solutions so all P problems belong to NP. But there were a lot of NP problems to which we didn't know polynomial ways to solve. The natural questions this raises is: are these problems really more difficult to solve or it's just a matter of finding better algorithms for them?
In other words, does P = NP?
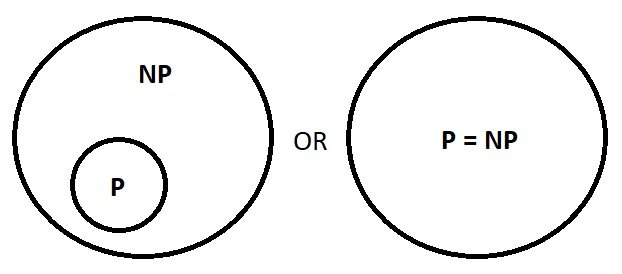
Which is the correct? (Source: myself)
The grand prize!
In 2000, the Clay Mathematics Institute has stated 7 mathematical problems so that anybody who solves one of them will win a grand prize of 1 million dollars! The P versus NP problem is one of them so if you want that money you will have to mathematically prove that as least one NP problem does not have a polynomial solution (P ≠ NP) or that all NP problems have those (P = NP).
This whole story might seem a little too abstract but if P=NP that would have a huge impact on the world we live today! Hard computer tasks would suddenly be feasible like for instance cracking a strong password which with brute force today could take billions of years on a supercomputer!
To be honest, most computer scientists believe that P ≠ NP, but it's not proved yet. Maybe we'll get a big surprise in the future! But whether is equal or not the P versus NP problem is still a very interesting dilemma. I hope you all liked this post and stay tuned for more :)
Til next time,
Anderson
Notations and concepts are very simplified here but you can check out other sources for a more complete understanding:
Article on Communications of the ACM Magazine
Good Explanation on MIT News
Book: Computational Complexity: A Modern Approach
Images for the thumbnail:
https://pixabay.com/en/background-circuit-grey-digital-2426329/
https://pixabay.com/en/cup-trophy-award-sport-profit-1015644/
https://pixabay.com/pt/jogos-mentais-mente-jogos-1917499/
My recent posts:
My first paper was accepted for IEEE conference in SPAIN!
DCS #3 - How can you do anything with 0s and 1s?
DCS #1 - Decomplicating Computer Stuff!
If you like this post, consider resteeming and sharing it with others! Also, comment below and be a part of this discussion!
Congratulations @urbanoanderson! You received a personal award!
Click here to view your Board of Honor
Congratulations @urbanoanderson! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Vote for @Steemitboard as a witness to get one more award and increased upvotes!