
Il caos è disordine, il caos è imprevedibile, il caos è non capirci un cazzo. Se fosse prevedibile sarebbe poco caotico. Eppure, eppure persino il caos si può studiare. Lo si può fare con modelli fisici e matematici.
Innanzitutto specifichiamo una cosa. In natura il caso esiste, a livello quantistico. Le particelle subatomiche sono soggette a fenomeni che sono intrinsecamente casuali. Questo significa che in certe condizioni non si può sapere a priori quale sarà l’esito di una misura che vogliamo effettuare su una particella.
Se parliamo del mondo macroscopico, ci è facile intuire che le proprietà di un corpo al tempo T saranno simili alle proprietà che aveva il corpo all’istante T-ε (T meno epsilon), con ε piccolo a piacere. Consideriamo ad esempio la velocità di un corpo in caduta libera. Questo sta accelerando, e diciamo che all’istante t possiede una velocità v. Se consideriamo la velocità in un istante immediatamente precedente (o successivo!) a t, allora il valore della velocità non si sarà discostato di molto. Questo ha perfettamente senso, in fondo, in un brevissimo istante di tempo quanto può accelerare il corpo? Molto poco.
Ecco, nel magico mondo delle particelle non funziona così. Possiamo fare una misura e ripeterla dopo un istante di tempo brevissimo, ma potremmo trovare un risultato completamente diverso dal precedente. Non solo. L’esito di questa misura è imprevedibile. Questo è il caos a livello quantistico.
Molto figo.
Nel mondo macroscopico gli effetti quantistici diventano assolutamente trascurabili.
Non è quello il caos che ci interessa. In effetti, il mondo macroscopico si comporta in maniera deterministica. Ossia, sapendo le leggi che governano la comportamento di ciò che volgiamo studiare, e conoscendo tutti i fattori in gioco, possiamo determinare lo stato del nostro oggetto di studio a qualsiasi tempo t. Questo in teoria, poi bisogna fare i conti con la realtà. Spesso i fattori che influenzano l’evoluzione di un sistema fisico sono talmente tanti che diventa impossibile tenerne il conto di tutti. Quindi il fatto che noi definiamo “caotico” un sistema è dovuto alla nostra limitatezza di esseri umani. Non possiamo conoscere tutto e con infinita precisione, di conseguenza da un certo istante in poi il sistema sembra assumere un comportamento casuale, anche se teoricamente non è così. Pensate alle previsioni del tempo.
C’è un motivo se dopo 3/4 giorni diventano poco affidabili. L’atmosfera è un sistema molto complicato, perché ogni molecola che la compone influenza il comportamento delle altre. Se volessimo delle previsioni del tempo praticamente perfette dovremmo conoscere la posizione, la massa e la velocità di ogni singola particella dell’atmosfera. Assolutamente impossibile. Avrete sentito parlare dell’effetto farfalla. Si dice che una farfalla che sbatte le ali in un posto X possa generare un uragano nel posto Y, distante migliaia di Km. È ovviamente un’esagerazione (?) ma l’idea che ci sta dietro è perfettamente sensata: una piccola alterazione delle condizioni iniziali può portare, dopo un certo tempo, a uno stato del sistema completamente diverso da quello che avremmo ottenuto se quell’alterazione non ci fosse stata. Alan Turing scrisse in un saggio:
“Lo spostamento di un singolo elettrone per un miliardesimo di centimetro, a un momento dato, potrebbe significare la differenza tra due avvenimenti molto diversi, come l'uccisione di un uomo un anno dopo, a causa di una valanga, o la sua salvezza.”.
Questo è un ulteriore motivo per impedisce la previsione a lungo termine (decine di giorni) del tempo meteorologico. Perché se oggi vi soffiate il naso a Bari potreste essere responsabili del temporale che si verificherà tra un anno a Milano.
Si chiama sensibilità alle condizioni iniziali, ed è tipica dei sistemi caotici.
Ho scritto all’inizio che il caos si può studiare. Vi ho in parte mentito. Si possono costruire modelli matematici semplificati che descrivono un sistema caotico, al quale vengono tolti vari effetti perturbativi. Oppure si possono costruire dei modelli generali, basati sull’osservazione ripetuta nel tempo di un fenomeno. Pensate ancora alle previsioni del tempo. Non possiamo sapere se il 24 luglio 2026 ci caldo o no, ma visto il periodo e considerando i dati storici, possiamo ragionevolmente supporre che non ci sarà freddo. Nonostante l’atmosfera sia un sistema caotico, si possono comunque elaborare modelli che descrivono piuttosto bene il sistema su larga scala, senza scendere nei dettagli. Possiamo quindi affermare che, anche se un sistema è caotico, non è detto che non si comporti secondo schemi che si ripetono.
In effetti, un sistema dinamico caotico può nel tempo evolvere, stabilizzarsi all’interno di una specifica regione e non uscire più da lì. Questa regione prende il nome di Attrattore strano.
Il primo esempio di attrattore strano fu proposto nel 1963 da Lorenz, un matematico americano.
Un piccolo passo indietro.
Per studiare il moto dei fluidi, vengono utilizzate le equazioni di Navier-Stokes. Sono delle equazioni differenziali alle derivate parziali. E già dal nome…Sono queste qua:
brutta roba. Così brutta che la loro risoluzione analitica ancora non è nota. È uno dei sette problemi del millennio. È però possibile semplificare queste equazioni, e darne una soluzione analitica. Oppure si possono inserire in un computer per calcolarne brutalmente il risultato.
Torniamo da Lorenz
Semplificò le equazioni di Navier-Stokes così tanto da ottenere un sistema di tre equazioni, decisamente più maneggiabile, eccolo:
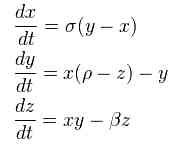
dove x,y,z sono tre coordinate, non per forza spaziali, ma per esempio, se parliamo di gas, temperatura, pressione e umidità. Le altre lettere rappresentano delle costanti di vario tipo.
Continuiamo con l’esempio del gas. Le equazioni descrivono l’evoluzione temporale delle coordinate dello stesso.
Supponiamo di avere due gas, che possiedono delle condizioni iniziali molto simili, ma non identiche. Come si evolve il sistema? All’inizio la differenza tra le coordinate è minima, ma dopo un certo tempo diventa davvero significativa. Questa è la dipendenza sensibile dalle condizioni iniziali, una piccola alterazione porta a risultati completamente diversi.
Se proviamo a fare un grafico, quello che salta fuori è una cosa del genere:
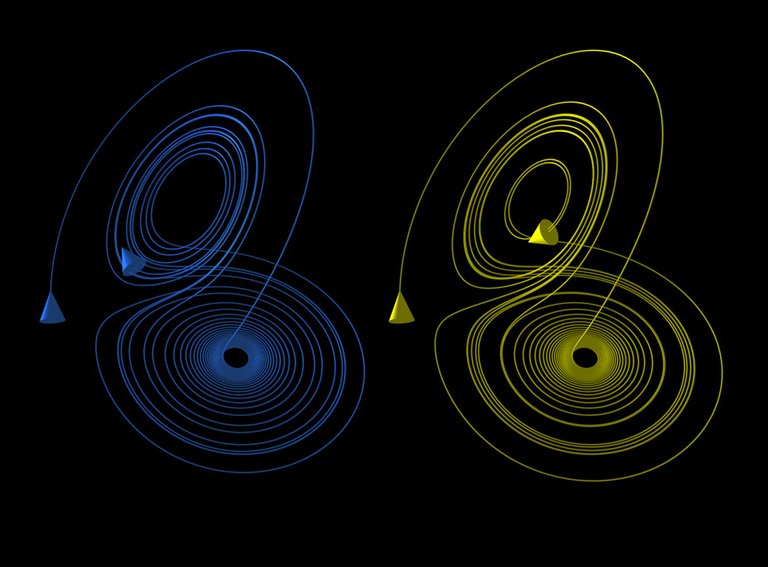
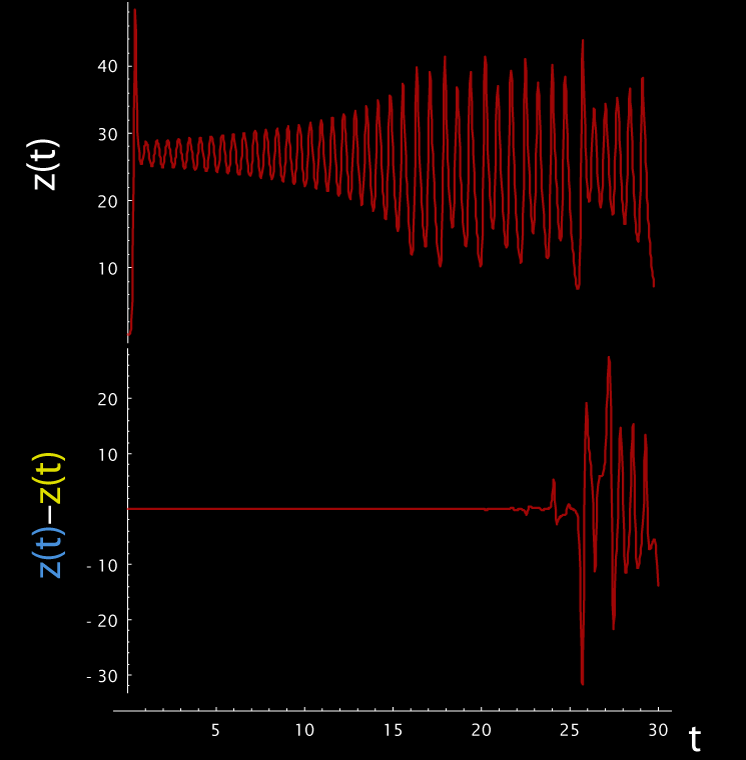
vedete? Vengono mostrati i due gas a momenti diversi. All’inizio non c’è quasi differenza, alla fine è ben evidente.
Le coordinate (termodinamiche) del gas cambiano in modo casuale, ma alla fine vanno a stabilizzarsi all’interno di quella figura, chiamata Attrattore di Lorenz. Immaginiamo di sovrapporre le due traiettorie, così:

poi osserviamo questa figura frontalmente:
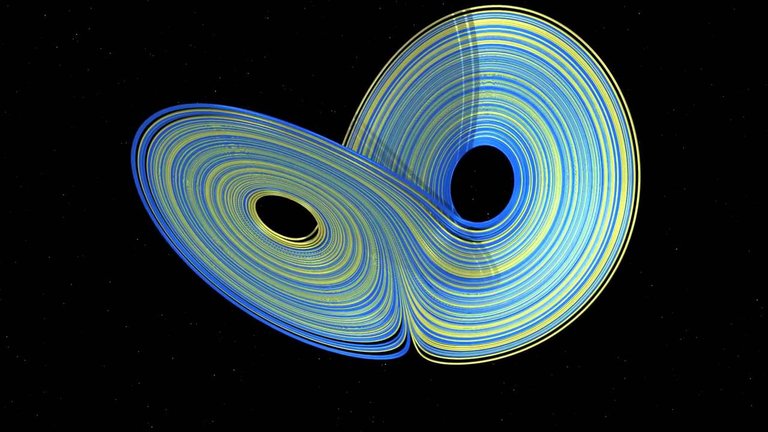
proprio una bella farfalla. In effetti, è proprio questo diagramma che dà il nome all’omonimo effetto.
Di attrattori ne esistono diversi, ma il succo della storia è il seguente: non possiamo studiare il futuro di un sistema per un tempo infinito, ma possiamo studiare l’attrattore di quel sistema, se esiste.
L’effetto farfalla ha avuto un’influenza notevole sulla cultura popolare, viene spesso citato in film e serie tv, ma anche libri e fumetti.
Però ne è stato studiato l’analogo anche nel cervello.
L’idea dei ricercatori dell'University College, è stata quella di stimolare un neurone con un impulso elettrico per osservare il comportamento del cervello. I casi possibili erano due: o l’impulso si sarebbe fermato dopo pochi neuroni, oppure avrebbe stimolato altri neuroni, che a loro volta ne avrebbero stimolati altri e così via. Buona la seconda. Dal primo neurone sono partiti una trentina di impulsi verso neuroni adiacenti, da questi un'altra trentina di impulsi, che hanno poi continuato a diffondersi. Questo è un indizio a supporto del fatto che nel cervello è presente un “rumore di fondo” costante, e che probabilmente per funzionare bene deve ignorare la variabilità del singolo neurone, e considerare invece l’attività dei gruppi di neuroni.
Secondo gli scienziati questo è un male necessario, sacrificato sull’altare dell’elevata connessione tra i neuroni. Poco male, il cervello funziona piuttosto bene.
Se l’effetto farfalla vi ha sconvolto, aspettate che vi parli della DIFFERENZIABILITA DI UNA MISURA o di SIGMA FINITEZZA. No scherzo, non lo farò mai. Ciao!
Amici che studiano matematica e:
http://www.chaos-math.org/it/chaos-vii-attrattori-strani
https://it.wikipedia.org/wiki/Effetto_farfalla
https://it.wikipedia.org/wiki/Attrattore_di_Lorenz
http://www.lescienze.it/news/2010/07/01/news/anche_il_cervello_ha_il_suo_effetto_farfalla_-555497/

Congratulazioni, hai ricevuto un voto anche da SteemStem!

L'effetto farfalla è una delle cose più interessanti e a cui ho pensato di più in vita mia... Tempo fa infatti avevo anche fatto un post a riguardo!
Uh me lo sono perso D:
Vado a leggerlo subito
Fantastico... mi hai ricordato le Equazioni di Navier-Stokes. Bell'articolo. Ora ti tocca parlare davvero di DIFFERENZIABILITA DI UNA MISURA o di SIGMA FINITEZZA.
Mai!
Te la sei cercata!!! ehehehe
Preferisco votarti quando ho un VP più alto, ma ho paura di dimenticarmi.
Naaa, vota vota :D
(Grazie)
Bravo! Ottima esposizione e argomento molto interessante ;)
La teoria del caos è stato l'argomento della mia tesina!
Grande :D
Chissà, magari un giorno la pubblicherai su Steemit.. ;)
Questo è l'indice!
Immagine.jpg
Non la pubblico perché è un contenuto lontano da ciò che in mente per Steemit. Ovviamente, trattai tutto a livello ultra-scolastico. L'idea mi venne grazie al videogioco Life Is Strange di cui puoi vedere una foto nel mio primo post.