-FIBONACCI
Leonardo Fibonacci nato a Pisa nel 1175 è considerato uno dei più grandi matematici di sempre.

fù il primo a introdurre i numeri arabo (0-1-2-3-4-5-6-7-8-9) in Europache introdusse nel I di XV capitoli scritti nella sua opera Liber Abbaci pubblicata nel 1202
-LA SUCCESSIONE DI FIBONACCI
la successione di Fibonacci nasce con l'intento di trovare una legge matematica che potesse descrivere la crescita della popolazione dei congili.
assumendo le seguenti condizioni:
•ogni coppia di conigli genera un’altra coppia di conigli alla volta;
•i conigli diventano fertili dopo un mese di vita;
•una volta fertili, ogni coppia di conigli genererà una coppia di conigli al mese.
se queste condizioni venivano rispettate si verificava quanto segue:
•il primo mese solo una coppia di conigli sarà fertile.
•il secondo mese ci saranno due coppie di conigli di cui però solo una fertile.
•il terzo mese ci saranno 2+1=3 coppie di conigli di cui solo due saranno fertili.
•il quarto mese le coppie di conigli saranno 3+2=5.
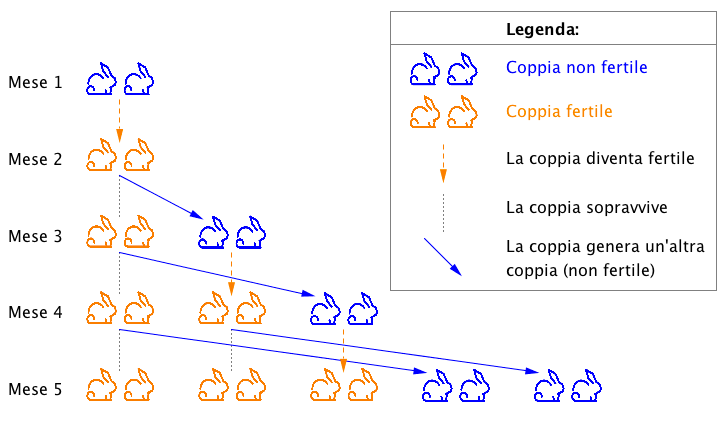
il numero di coppie di conigli esprime in qeusto modo la successione di fibonacci:
1,1, 2, 3, 5, 8, 13, 21, 34, 55....
in pratica un numero di Fibonacci non è altro che la somma dei due numeri precedenti ad esso.

CORRELAZIONE TRA LA SEZIONE AUREA E FIBONACCI
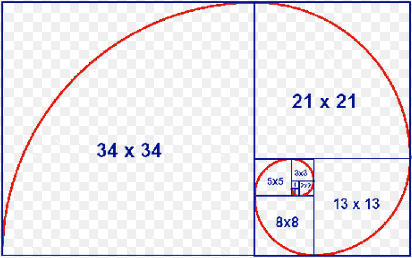
Keplero scoprì che il rapporto fra due numeri consecutivi della successione di Fibonacci approssimava via via, sempre più precisamente, il numero aureo

cioè:
1,6180339887498948482045868343656381177203091798057628621354486227052604628189024497072072041893911374847540880753868917521266338622235369317931800607667263544............
CORRELAZIONE TRA IL TRIANGOLO DI TARTAGLIA E FIBONACCI
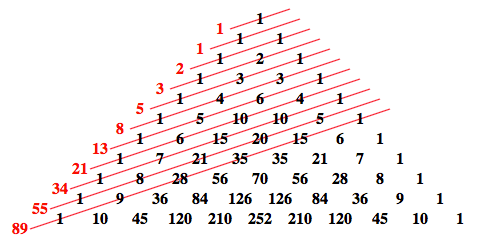
La successione ottenuta considerando la somma dei termini presenti su ciascuna “diagonale” del triangolo di Tartaglia corrisponde alla successione di Fibonacci.
ALCUNI ESEMPI DELLA RICORRENZA DEI NUMERI DI FIBONACCI IN VARI SETTORI
•in chimica
Nel 2010 alcuni scienziati dell'università di Oxford hanno osservato come in un composto chimico di niobato di cobalto, portato in maniera artificiale in uno stato quantistico critico, appare una simmetria riconducibile al gruppo di Lie E8, con due picchi alle basse energie in un rapporto simile a quello aureo.
•nella musica
Sul piano compositivo, attraverso la successione di Fibonacci, la sezione aurea può essere rapportata a qualsiasi unità di misura riguardante la musica ad esempio la durata temporale di un brano il numero di note o di battute la durata temporale di una certa nota ecc.....
•in botanica
Quasi tutti i fiori hanno 3(gigli), 5(ranuncoli), 8(delphinium), 13(calendula), 21(l'astro), 34-55-89(margherite) petali.
I pistilli sulle corolle dei fiori spesso si dispongono secondo uno schema di spirali il cui numero corrisponde ad uno della successione di Fibonacci, di solito le spirali orientate in senso orario sono 34 mentre quelle orientate in senso antiorario 55, altre volte sono rispettivamente 55 e ottantanove, o 89 e 144.
I numeri di Fibonacci sono presenti anche nel numero di infiorescenze di ortaggi come il Broccolo romanesco.

•nel corpo umano
Il rapporto fra le lunghezze delle falangi del dito medio e anulare di un uomo adulto è aureo, come anche il rapporto tra la lunghezza del braccio e l'avambraccio, e tra la lunghezza della gamba e la sua parte inferiore
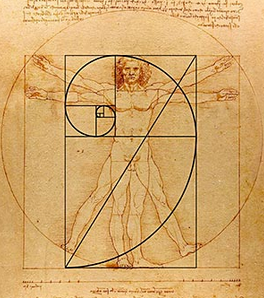
•in natura
è pieno di esempi in cui ricorre la sequenza di fibonacci, il più eclatante è la conchiglia:

•IN ECONOMIA
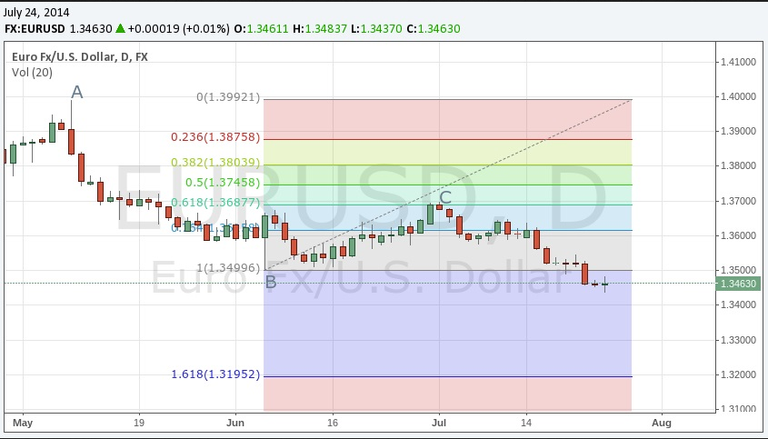
I numeri di Fibonacci sono utilizzati anche in economia nell'Analisi tecnica per le previsioni dell'andamento dei titoli in borsa, secondo la teoria delle onde di Elliott, l'unico metodo in grado di individuare un movimento del mercato dall'inizio alla fine e quindi di presumere i futuri andamenti dei prezzi.
FARO' UN'ARTICOLO PIU' DETTAGLIATO A RIGUARDO, in cui spieghero come usare fibonacci sui grafici
Incredibile! Chissà quali altri applicazioni dobbiamo ancora scoprire!
Le foto ed i diagrammi da dove arrivano? Dove le hai trovate?