

Muchas veces es necesario usar métodos numéricos para poder encontrar una solución aproximada de algunos problemas en diversas áreas de la ciencia y la ingeniería. Muchos de esos problemas como ya hemos visto anteriormente en mis otras publicaciones (Aplicaciones de las Ecuaciones Diferenciales Ordinarias | Lección #8, Aplicaciones de las Ecuaciones Diferenciales Ordinarias | Lección #9, Aplicaciones de las Ecuaciones Diferenciales Ordinarias | Lección #10, Aplicación de la Ecuaciones Diferenciales Ordinarias a la Biología Marina) se pueden modelar usando ecuaciones diferenciales.
Existen muchos métodos numéricos para abordar la aproximación de soluciones de estas ecuaciones, hoy abordaremos dos de estos métodos, a saber:
- el Método en Diferencias Finitas (MDF) y
- el Método de los Elementos Finitos (MEF).
En general, podemos decir, que estos métodos son unos de los más usados, y es por ellos que algunos autores los han llamados "métodos clásicos". Los mismos podemos decir, que tienen sus ventajas y desventajas sobre el otro, dependiendo del tipo de problema que se desee resolver.

El Problema Modelo
Consideremos la siguiente ecuación:

sujeto a las condiciones de frontera
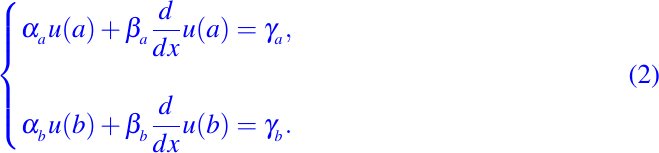
Básicamente la ecuación mostrada en (1) describe la propagación del calor, a través de la convección - difusión en régimen estacionario. La función u(x) describe la temperatura en cualquier punto de su domino, k(x)>0 describe el coeficiente de difusión térmica, v(x) es la velocidad de convección (o advección) y f(x) es una función escalar que describe la existencia de una fuente o sumidero para el problema. Los parámetros

toman diferentes valores dependiendo de las condiciones de frontera, es decir, condiciones de frontera Dirichlet, Neumann o Robin.
Notemos que la solución a la ecuación descrita en (1) sujeta a las condiciones de contorno dadas en (2) la podemos encontrar explícitamente mediante métodos analíticos. Sin embargo, usaremos fuertemente este hecho para establecer un cuadro comparativo entre los métodos numéricos ya mencionados.

Métodos Numéricos
Vamos a describir muy brevemente los métodos que usaremos para realizar la comparación de los métodos, los lectores interesado en estudiar con detalles los métodos que estamos usando, pueden consultar las siguientes referencias:
- Strikwerda, John C. Finite difference schemes and partial differential equations. Vol. 88. SIAM, 2004.
- Ŝolín, Pavel. Partial differential equations and the finite element method. Vol. 73. John Wiley & Sons, 2005.
Método en Diferencias Finitas (MDF)
Ahora bien, el Método en Diferencias Finitas consiste en la discretización de los operadores diferenciales involucrados en el problema, suponiendo el dominio físico lo podemos discretizar en una malla que consta de n+1 nodos o puntos de malla, es decir, xi como lo podemos apreciar en la figura siguiente:

Malla Unidimensional para el Método en Diferencias Finitas. Elaborado por @abdulmath con

Usando desarrollos de Taylor, podemos obtener las siguientes fórmulas para la primera y segunda derivada de la solución que queremos encontrar del problema, a saber:
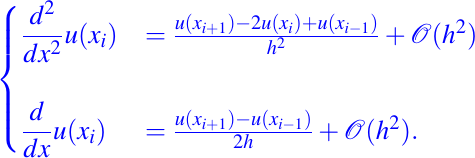
Ahora, restringiendo nuestra atención a la ecuación (1) con las condiciones de contorno de Robin (2), entonces al aplicar el método de diferencia finita obtenemos el siguiente esquema para el cálculo de la solución numérica del problema de valores en la frontera dado en (1)-(2), como lo mostramos a continuación:
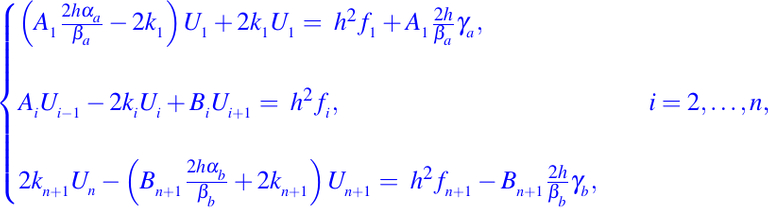
donde

Método de los Elementos Finitos (MEF)
Supongamos, que ya hemos definido un problema concreto. El método de los elementos finitos consiste en hallar la solución de ese problema de la forma

donde los coeficientes ai son desconocidos y deben determinarse a lo largo de un proceso iterativo. Las funciones forman una base para un espacio finito dimensional

y este es el espacio de las funciones adecuadas que resuelven la versión débil o forma variacional del siguiente problema, en nuestro caso elegiremos a este espacio de funciones como un espacio de Sobolev,
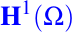
la formulación variacional es:

donde el funcional bilineal B(u(x),s(x)) y el funcional lineal l(s(x)) vienen dado por:
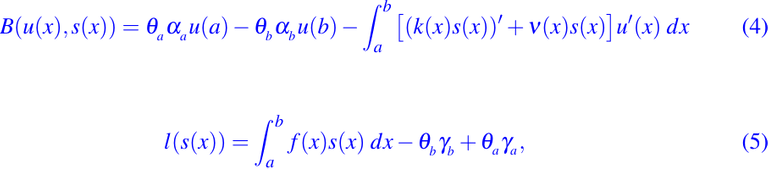
donde


Resultados Numéricos
Recordemos que nuestro problema de frontera es de la forma presentada en (1)-(2) cuyo dominio es el intervalo [0,1]. El error los estimaremos utilizando las normas siguientes:
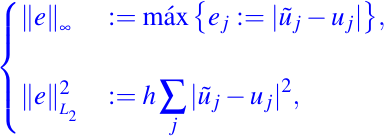
donde uj con tilde denota la solución numérica obtenida por alguno de los métodos numéricos mencionadas anteriormente y uj denota la solución exacta del problema de frontera (1)-(2).

Experimento 01
Consideremos el problema de frontera dado por (1)-(2) con coeficiente de difusión k=1, velocidad convectiva v=0, condiciones de frontera de Robin de la forma siguiente:
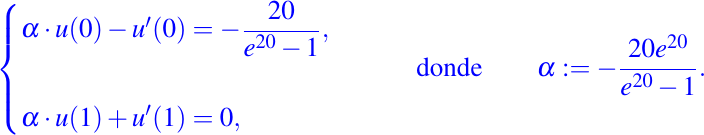
y el término fuente f(x) se define de tal manera que la solución exacta está dada por
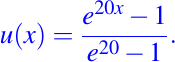
A continuación mostraremos cuatro gráficos, donde mostraremos la solución exacta, la solución aproximada con el método en Diferencias Finitas y el método de los Elementos Finitos, con una malla compuesta con 10, 20, 50, y 100 nodos o puntos de malla respectivamente:
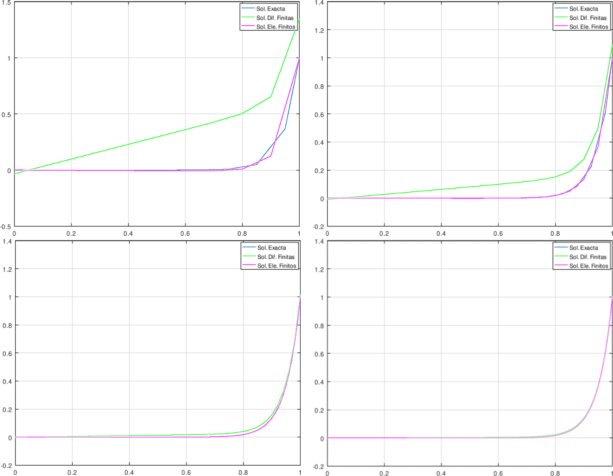
Gráficos elaborados con GNU-Octave. Elaborados por @abdulmath.
Como podemos apreciar, cuando la malla tiene pocos nodos o puntos de mallas, la solución aproximada usando el método de los elementos finitos se acerca más visualmente, sin embargo más adelante veremos que no es tan así, de la misma manera vemos que la aproximación usando el método en Diferencias Finitas, sin embargo cuando aumentamos la cantidad de nodos mejora mucho la aproximación.
En las siguientes gráficas mostramos el grado de convergencia de los métodos, así como una tabla donde se muestran los cálculos del orden de convergencia con las diferentes normas.
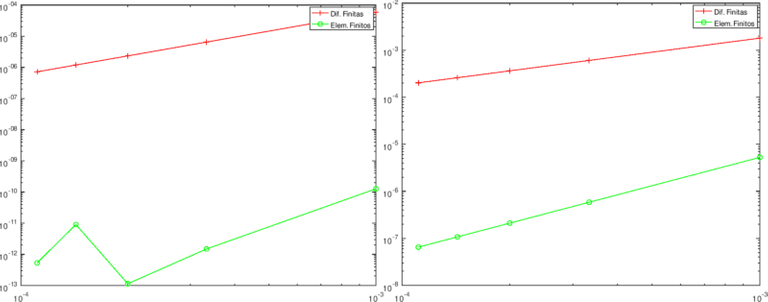
Gráficos elaborados con GNU-Octave. Elaborados por @abdulmath.
| # nodos | MDF (Máx) | MEF (Máx) | MDF (L2) | MEF (L2) |
|---|---|---|---|---|
| 1000 | 1.999944 | 4.000306 | 0.986027 | 1.999880 |
| 3000 | 1.999990 | 4.022705 | 0.994014 | 1.999978 |
| 5000 | 1.999998 | 3.485599 | 0.997404 | 1.999996 |
| 7000 | 2.000000 | -10.558 | 0.998307 | 1.99996 |
| 9000 | 1.999999 | 15.251 | 0.998740 | 2.000043 |
Como podemos apreciar, la norma del máximo para este problema con el método de elementos finitos presenta una super-convergencia que alcanza el epsilon máquina. Por lo tanto, las oscilaciones que tienen el gráfico en el caso del método de elementos finitos se deben a los errores de redondeo lo que causa pérdida de precisión de la máquina para el método de los elementos finitos.

Experimento 02
Consideremos el problema de frontera dado como en (1)-(2), donde el coeficiente de difusión esta dado por
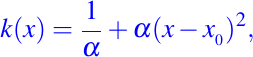
la velocidad convectiva esta dada por:
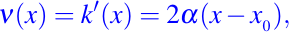
con

y las condiciones de frontera tipo Robin dadas por
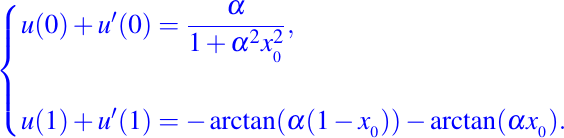
La función fuente f(x) se determina de tal manera que la solución analítica de nuestro problema sea:

Es las gráficas anexas, comparamos la solución exacta contra la solución aproximada para mallas uniformes con 10, 20, 50, 60, 80, y 100 nodos o puntos de mallas. Como podemos observar, las primeras gráficas muestra comportamientos oscilatorios para la solución aproximada usando el método en Diferencias Finitas, a medida que se aumentan los nodos en la malla, el movimiento oscilatorio desaparece, tal cuál lo podemos apreciar a continuación:
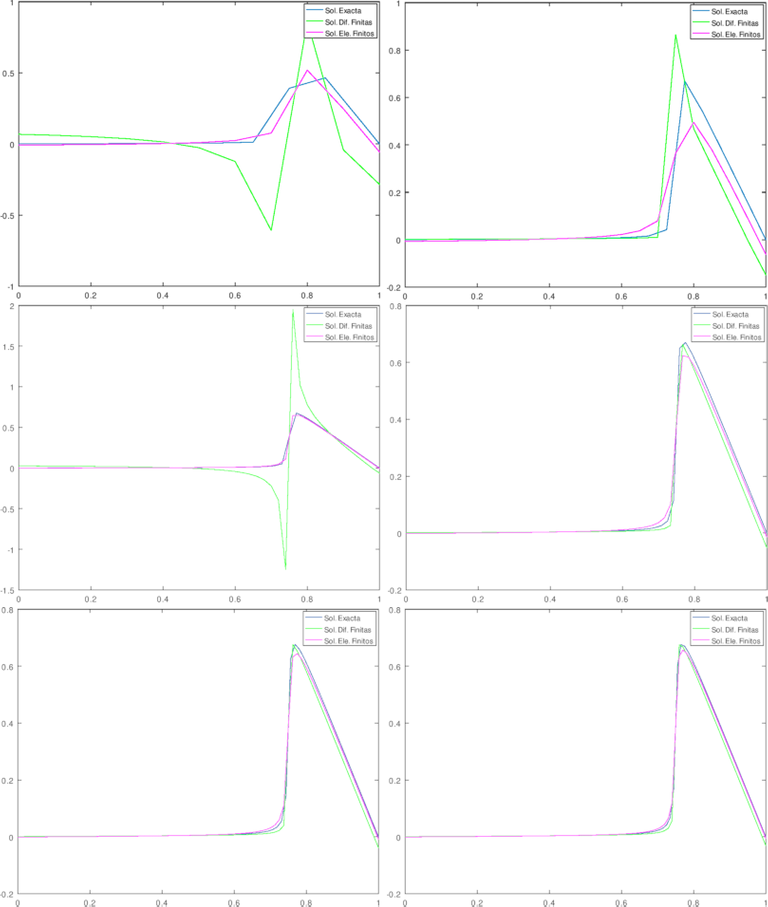
Gráficos elaborados con GNU-Octave. Elaborados por @abdulmath.
A continuación mostramos el grado de convergencia de los métodos, así como una tabla donde se muestran los cálculos realizados.
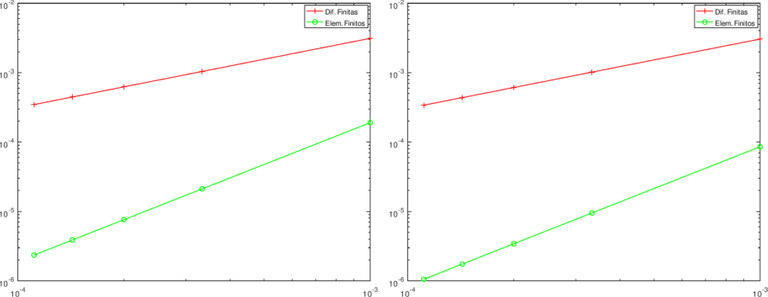
Gráficos elaborados con GNU-Octave. Elaborados por @abdulmath.
| # nodos | MDF (Máx) | MEF (Máx) | MDF (L2) | MEF (L2) |
|---|---|---|---|---|
| 1000 | 1.154080 | 1.993329 | 1.004321 | 1.996938 |
| 3000 | 1.000175 | 1.998233 | 0.998419 | 1.998873 |
| 5000 | 1.000073 | 1.999533 | 0.998652 | 1.999803 |
| 7000 | 1.000047 | 1.999993 | 0.999021 | 1.999919 |
| 9000 | 1.000035 | 1.999783 | 0.999236 | 1.999950 |

Algunas Consideraciones
- Resulta claro, que el MEF presenta mejores resultados en precisión y convergencia que el MDF.
- En gran medida, se ha justificado el uso de MEF ante MDF en cuanto a la precisión del mismo, pero el MEF envuelve una complejidad teórica grande, para aquellos que no son matemáticos. Tal dificultad se acrecienta, si requiere aumentar la precisión y el orden de convergencia del método, sin embargo el MEF lo logra con mucha facilidad.
- Además, hay que añadir que existe una eficiente implementación computacional, pues el uso de matrices para definir operadores y condiciones de contorno puede resultar en un rápido desbordamiento de memoria en el método MDF.
- Otro aspecto que vale la pena mencionar es el alto grado de complejidad y dificultad que presenta MDF para trabajar en mallas que se ajusten a dominios cuyas geometrías son arbitrarias.

Queridos amigos y lectores, espero hayan disfrutado de esta publicación en la cual mostramos la eficiencia y precisión, así como el orden de convergencia de los métodos ya mencionados. Espero que esto pueda servir de apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas y sus aplicaciones. No olviden dejar sus comentarios. Saludos y nos leemos pronto.
Si desean consultar un poco más del tema pueden usar las siguientes referencias.
- Strikwerda, John C. Finite difference schemes and partial differential equations. Vol. 88. SIAM, 2004.
- Ŝolín, Pavel. Partial differential equations and the finite element method. Vol. 73. John Wiley & Sons, 2005.
Las imágenes, separadores y las ecuaciones fueron creadas y editadas con  , y GIMP. Los gráficos y cálculos fueron realizados con GNU-Octave. Elaborados por @abdulmath. El software usado es completamente Software Libre.
, y GIMP. Los gráficos y cálculos fueron realizados con GNU-Octave. Elaborados por @abdulmath. El software usado es completamente Software Libre.

Imagen elaborada por @abdulmath, diseñadas y editada con Karbon y GIMP.
Saludos estimado amigo @abdulmath, observo en esta nueva temática la inclusión de imágenes gráficas, elemento que ayuda a la comprensión de contenido.
Saludos @lupafilotaxia, claro, en la medida que el tema lo permita, se pueden ir agregando gráficos para mostrar algunos resultados que se comentan en la publicación. Agradecido por tu valoración. Saludos y un abrazo.
excelente Post. Muy interesante, buena presentaci[on y muy completo.
Profe me quito el sombrero
Hola @geadriana, gracias por tu comentario y valoración, y aprecio tu visita a mi blog, al igual que tus publicaciones son de excelente calidad. Saludos y un abrazo.
Congratulations @abdulmath! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
Do not miss the last post from @steemitboard:
SteemitBoard World Cup Contest - Brazil vs Belgium
Participate in the SteemitBoard World Cup Contest!
Collect World Cup badges and win free SBD
Support the Gold Sponsors of the contest: @good-karma and @lukestokes
La incorporación de gráficas de curvatura, agregan una nueva dimensión a tus publicaciones..! ¡Votado por Engranaje!
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Thanks for the support
Hi @abdulmath!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Thanks for the support
Abdul, hermano, excelente trabajo. Es un método muy utilizado en distintas ramas de la ingeniería. Resulta interesante y atractiva su aplicación sobretodo a nivel de simulaciones y diseño. En verdad te felicito, hermano. Apartando el tema, te invito a que leas algo sencillo, pero interesante, sobre el "Índice Big-Mac" a propósito de que Venezuela fue excluida de la lista en 2018 (visita mi blog). Te deseo mucho éxito y te sigo.