Hola;
Llegue hasta ti mi saludo de gratitud y de buenos deseos. Deseando llevar a cabo una visión compartida, sigo entregándote este compendio de información para que sigamos en la vía de los símbolos matemáticos.
Continuamos con el Cálculo proposicional. Conectivos lógicos.
En esta sesión seguimos desarrollando parte del “cálculo proposicional”, en lo que concierne a las “operaciones verificadoras” teniendo en cuenta los “conectivos lógicos”. Entonces comencemos por definir cada conectivo lógico.
El primero y más sencillo es “la negación”.
Supongamos que “p” simboliza a una proposición. Entonces la NEGACIÓN de “p” es la proposición que se simboliza por “ ~p” y a la cual leeremos “no p”, pero que es más usual traducirla como “no es cierto que p”, “no es verdad que p”, “es falso que p”. En este orden de ideas podemos traducir al símbolo "~" como “no es cierto que”, “no es verdad que”, “es falso que”
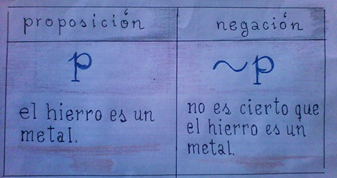
Como vemos, la proposición es
p : el hierro es un metal. Entonces su negación es ~p, la cual no tiene coherencia si decimos “no el hierro es un metal”. Es por ello que se escribe “no es cierto que el hierro es un metal”, aunque también tiene validez, y es más cómodo, escribir “el hierro no es un metal”, además de las otras traducciones vistas anteriormente.
Es fácil verificar que si “x” es una proposición verdadera, entonces “ ~ x” es falsa, y viceversa. Este hecho nos lleva a definir la operación verificadora
VL(~x) = 1 – VL(x). O su equivalente VL(x) = 1 – VL(~x)

De acuerdo a la fórmula anterior y considerando a "x" como una proposición dada ¿Te atreverías a demostrar que VL(~(~ x)) = VL(x) ?
De aquí podríamos asegurar que “negar a la negación de una proposición equivale a la misma proposición”. Esto es; si “x” es una proposición, entonces ~(~ x) ≡ x, esta “propiedad” se conoce como la “doble negación”.
Por ejemplo; sea la proposición p: La vida es una sola.
Entonces ~ p : La vida no es una sola.
Luego, ~(~ p) : no es cierto que la vida no es una sola.
Esto último, quiere decir que la vida es una sola.
O sea, ~(~ p) ≡ p.
Ahora vamos a proseguir con “la conjunción”.
Supongamos que “p” y “q” simbolizan a dos proposiciones.
La CONJUNCIÓN de “p” y “q” es la proposición que se simboliza por
“p ∧ q” y que leeremos “p y q”.
Puede comprobarse que la conjunción es “conmutativa”,
esto es; “p ∧ q” equivale a “q ∧ p”, en términos matemáticos
p ∧ q ≡ q ∧ p.
Veamos el siguiente ejemplo:
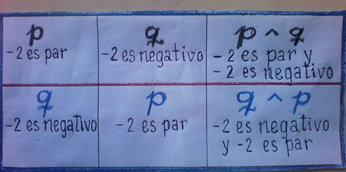
La conjunción como operación verificadora se rige por la fórmula
VL(p ∧ q) = mín{ VL(p), VL(q)}
En donde "p" y "q" son proposiciones.
La expresión de la derecha de la igualdad quiere decir “el mínimo de los valores lógicos de”p” y de “q”.
¿Podrías deducir en qué caso p ∧ q es verdadera?
Vemos otro ejemplo: Si tenemos las proposiciones
p : El oxígeno es un gas. Entonces VL(p) = 1
q : 3,1416 es un número irracional. Entonces VL(q) = 0
Por lo tanto; VL(p ∧ q) = mín{ VL(p), VL(q)} = mín{ 1 , 0 } = 0.
Así, p ∧ q : El oxígeno es un gas y 3,1416 es un número irracional. Es una proposición falsa.
Ya con todo esto, no insistiremos más sobre la negación y la conjunción, pues espero dejarte una inquietud para que seas tú quien profundice sobre estos temas.
Espero un próximo encuentro en donde seguiremos abordando otros conectivos lógicos con sus operaciones verificadoras… Hasta pronto…
<<<<< --------------- o0o0o0o0o0o0o0 --------------- >>>>>
Solo hay dos formas de vivir la vida: una, es pensando que nada es un milagro y la otra, es creer que todo lo es. -Albert Einstein-

Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app
app and including @stemsocial as a beneficiary to get a stronger support.
Congratulations @alezullysandro! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOP