¡En hora buena…!!
Mi saludo cordial y afectuoso, el cual refleja la alegría de sentir que todavía sigues este humilde proyecto.
Es por ello que considero propicio compartir la siguiente frase del Físico Estadounidense Richard Phillips Feynman:
“Las matemáticas son uno de los descubrimientos de la humanidad. Por lo tanto, no pueden ser más complicadas de lo que los hombres son capaces de comprender.”
Así que no hay impedimento para seguir adelante.
Cálculo proposicional. Conectivos lógicos.
En esta ocasión se tratará como temas a los conectivos lógicos la “disyunción inclusiva” y la “disyunción exclusiva”.
“La Disyunción Inclusiva” o simplemente “La Disyunción”.
Sean “p” y “q” las simbolizaciones de dos proposiciones.
Entonces la DISYUNCIÓN de “p” y “q” es la proposición que se simboliza por “ p ∨ q ” y a la cual leeremos “ p o q ”.
A semejanza de la conjunción, la disyunción también es “conmutativa”, esto es; decir “p ∨ q” equivale a decir “q ∨ p”, en otros términos, p ∨ q ≡ q ∨ p.

Así que es el símbolo “ ∨ ” el que se traduce como “ o ”.
La operación verificadora de la disyunción está dada por la fórmula:
VL(p ∨ q) = max{ VL(p), VL(q)}
Teniendo en cuenta que la expresión de la derecha de la igualdad quiere decir “el máximo de los valores lógicos de “p” y de “q”.
También podemos hablar de una “tabla de verdad” de la disyunción.
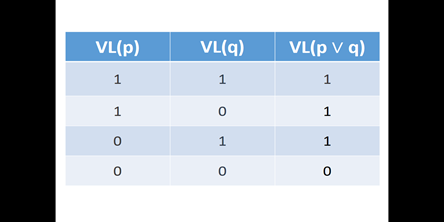
Vemos un ejemplo: Si tenemos las proposiciones
p : Existen números enteros entre 0 y 1. Entonces VL(p) = 0
q : Todos los números pares son racionales. Entonces VL(q) = 1
Entonces VL(p ∨ q) = max{ VL(p), VL(q)} = max{ 0 , 1 } = 1.
Compare estos resultados con la tabla de verdad.
Así, la proposición
p ∨ q : Existen números enteros entre 0 y 1 o Todos los números pares son racionales, es verdadera.
Es natural pensar: para que la disyunción sea verdadera, una de las proposiciones debe ser verdadera. Pero no es así, por eso decimos “Disyunción Inclusiva” porque incluye la posibilidad de que las dos proposiciones sean verdaderas para que la disyunción lo sea. Vea la tabla de verdad anterior.
Recordemos una definición que incluye este conectivo lógico:

“La Disyunción Exclusiva”
Supongamos que “p” y “q” simbolizan a dos proposiciones. Entonces la DISYUNCIÓN EXCLUSIVA de “p” y “q” es la proposición simbolizada por “ p ⊔ q ” y a la cual leeremos “ o p o q ”. También la disyunción exclusiva es “conmutativa”, lo cual lo podemos expresar como p ⊔ q ≡ q ⊔ p.

Así que es el símbolo “ ⊔ ” el que se traduce como “ o … o … ”
NOTA: el verdadero símbolo de la disyunción exclusiva es el que aparece en las imágenes, por razones de reconocimiento del editor de texto hemos colocado ⊔.
La operación verificadora de la disyunción exclusiva está dada por la fórmula:
VL(p ⊔ q) = | VL(p) - VL(q)|
La expresión de la derecha de la igualdad quiere decir “el valor absoluto de la resta de los valores lógicos de “p” y de “q”.
También tenemos la “tabla de verdad” de la disyunción exclusiva.
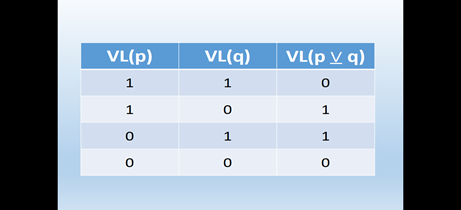
Un ejemplo: Con las proposiciones
p : Los números positivos son mayores que 0. Entonces VL(p) = 1
q : 2,7182 es un número positivo. Entonces VL(q) = 1
Entonces VL(p ⊔ q) = | VL(p) - VL(q)| = | 1 - 1| = 0.
Así, la proposición
p ⊔ q : O los números positivos son mayores que 0 o 2,7182 es un número positivo, es falsa.
En este ejemplo vemos que, aun siendo las proposiciones verdaderas, la disyunción exclusiva de ellas es falsa. Es por ello que decimos “Disyunción Exclusiva” porque excluye la posibilidad de que las dos proposiciones sean verdaderas para que VL(p ⊔ q) sea verdadera. O sea, o una es verdadera o lo es la otra. Consulta la tabla de verdad.

Seguimos insistiendo en dejarte la inquietud para que profundices más sobre estos temas.
Te espero en el próximo encuentro para que finalicemos con los conectivos lógicos y sus operaciones verificadoras… Hasta pronto…
<<<<< x x x --------------- 0 o 0 o 0 o 0 o 0 o 0 --------------- x x x >>>>>>
“Los encantos de esta ciencia sublime, las matemáticas, sólo se le revelan a aquellos que tienen el valor de profundizar en ella”
-Carl Friedrich Gauss-

Hola, Te invito también a unirte a nuestra comunidad aquí. Un grupo que se dedica a estudiar las palabras de Dios a través de las enseñanzas del hermano Eli Soriano.
¡Pregúntele al hermano Eli, la Biblia responderá!👇👇👇
https://peakd.com/c/hive-182074/created
Congratulations @alezullysandro! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @hivebuzz:
¡Felicitaciones!
1. Invierte en el PROYECTO ENTROPÍA y recibe ganancias semanalmente. Entra aquí para más información.
3. Suscríbete a nuestra COMUNIDADEntra aquí para más información sobre nuestro trail., apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática.
4. Creación de cuentas nuevas de Hive aquí.
5. Visita nuestro canal de Youtube.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA