Hola; gracias por estar de nuevo por aquí, me alegra que continúes en este compartir de ideas, pues tu visita me llevará a seguir adelante con este humilde proyecto que está puesto a la voluntad de Dios. Nuevamente gracias y, Bienvenido...!!!
LOS SÍMBOLOS MATEMÁTICOS.
... Continuación.
En la sesión anterior se hizo mención a los símbolos de las operaciones matemáticas “suma o adición”, “resta o sustracción”, “producto o multiplicación” “cociente o división”, “la potenciación”, “la radicación” y “los logaritmos”. Ahora vamos a considerar otros símbolos que nos indican el nombre de los conjuntos numéricos que estudiamos desde los primeros niveles hasta los estudios universitarios.
Comencemos con el “conjunto de los números naturales”.
A tal conjunto se le conoce o se simboliza con N.

Me atrevería a asegurar que usted dirá: “se toma la letra N para nombrar a estos números por ser la primera de la palabra naturales”, y en este contexto usted tiene razón, pues hay muchos autores que comparten esta afirmación.

Muchas veces se comete el error de considerar a los números naturales solo a estos que se presentan en la imagen de arriba, y este error se intenta justificar debido a que los demás números naturales, que son infinitos, surgen de la combinación precisa de ellos agrupándolos según los “dígitos” o “cifras”. En una próxima sesión se tocará esta construcción de los números naturales.
Ahora bien, según la historia de los números, debido a ciertas insuficiencias de los números naturales, surge la necesidad de “crear” otro tipo de números el cual lo conocemos como el “conjunto de los números enteros” y al cual lo simbolizamos con Z.
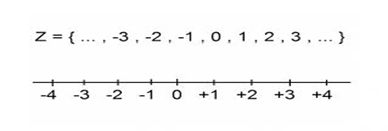
La Z es tomada de la palabra alemana “Zahl” que significa “número” o su variante “Zahlen” cuya traducción se refiere a “números”.
Dentro de este conjunto Z se identifican a los números naturales N como el conjunto Z+ de los números enteros positivos, y a Z- como el conjunto de los enteros negativos, mientras que Z* o Z - {0} representa al conjunto de los enteros excepto el cero. También encontramos, aunque no es muy usual, a los conjuntos de la forma nZ que simbolizan a los “múltiplos y submúltiplos de n”, por ejemplo,
5Z = {…-30,-25,-20,-15,-10,-5,0,+5,+10,+15,+20,+25,+30…}
Siguiendo por la historia de los números, de nuevo se presenta una deficiencia y en este caso es por parte de los números enteros, esto origina el surgimiento del conjunto Q de los “números racionales” los cuales por ser el resultado de una división de números enteros se toma su simbología de la palabra “Quotient” de algunos idiomas europeos, la cual significa “cociente”.

A semejanza de los números enteros, Q- hace referencia a los racionales negativos, Q+ a los racionales positivos y Q* o Q - {0} a los racionales sin el cero.
Hasta este momento vamos viendo que, como conjuntos, N “está contenido en” Z y Z “está contenido en” Q, lo cual se escribe así: N ⊂ Z ⊂ Q en donde "⊂" significa “está contenido en” o “es subconjunto de”. Así N ⊂ Z ⊂ Q quiere decir que los números naturales son también enteros y racionales, y los números enteros son racionales.
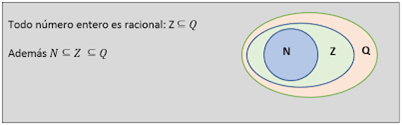
También el conjunto Q presentó deficiencias, por lo que se recurrió a definir al “conjunto de los números irracionales” como aquellos números que no son racionales, es decir, que no son naturales, ni enteros, ni racionales y que se simbolizarían con I.
Viéndolo de esta manera, los números racionales e irracionales son “disjuntos”, es decir, si un número es racional, entonces no es irracional y viceversa. Entonces la unión de los números racionales e irracionales conforma un conjunto numérico más extenso al cual llamaremos el “conjunto de los números Reales” y por razones obvias se representa con R, y de aquí es que muchos autores representan a los números irracionales como R – Q que quiere decir “los números reales sin los racionales”.

Hasta este momento podemos considerar que el mayor conjunto numérico que existe son los números reales R, pues hemos visto que contiene a todos los números conocidos, pero no es así, porque existe un tipo de número que son más complejos, de allí su nombre; “números complejos” los cuales se simbolizan por C y se definen como “pares ordenados”, “forma binómica” o “forma trigonométrica”, y como podrán darse cuenta, estos nombres impactan.
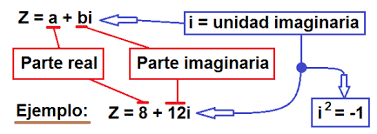
Que maravilloso como en unos minutos nos hemos paseado por los conjuntos numéricos recordando sus notaciones. Con esta sintonía esperamos un próximo encuentro en donde podremos tratar cómo se relacionan los números con ellos mismos, con los conjuntos numéricos y algo más.
La invitación está abierta para otra sesión en la que compartamos una pequeña parte del mundo de los símbolos matemáticos…
-∞……………………….…………………..+∞
Mi agradecimiento y créditos a “Pixabay.com” y “google.com/imágenes” de allí son tomadas las imágenes.
¡Felicitaciones!
1. Invierte en el PROYECTO ENTROPÍA y recibe ganancias semanalmente. Entra aquí para más información.
3. Suscríbete a nuestra COMUNIDAD, apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
4. Creación de cuentas nuevas de Hive aquí.
5. Visita nuestro canal de Youtube.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Excelente aporte, te recomendamos que coloques una foto de perfil para seguir recibiendo nuestro apoyo en futuras publicaciones.
att equipo de curación PROPIAMENTE
#entropia
@entropia
Congratulations @alezullysandro! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
You can view your badges on your board And compare to others on the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
Do not miss the last post from @hivebuzz: