Hola; que alegría encontrarnos de nuevo, tu participación me invita a una visión compartida. Mi más cordial saludo de bienvenida y sigamos adelante...!!
LOS SÍMBOLOS MATEMÁTICOS.
Seguimos...
En este momento nos proponemos a conocer o reconocer los símbolos que nos permiten resumir ciertos términos usados por los matemáticos en los cálculos o demostraciones de “teoremas”, “corolarios” o “lemas”, así como en las definiciones de estructuras matemáticas de un nivel avanzado. Veamos un ejemplo que considero clásico cuando se trata de expresar simbólicamente una definición:
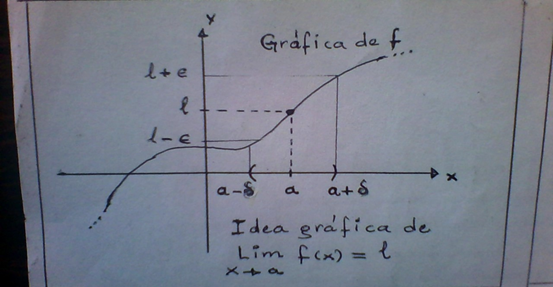
∀ϵ > 0, ∃δ = δ(ϵ) > 0 ∕ 0 < |x - a| < δ ⇒ | f(x) - l | < ϵ
Esta simbología define a Lim_(x⟶a ) f(x)=l que quiere decir “el límite de f(x) cuando x se aproxima a "a" es l ”. Esta definición es muy conocida por los que hayan cursado “cálculo I”, como pueden darse cuenta es una notación impactante, por lo que me atrevo a afirmar que causa orgullo reconocer lo que se está diciendo allí, este es uno de los objetivos de todo lo que hemos venido estudiando hasta esta sesión, además de motivar al lector para que pueda usar y reconocer lo que se quiere expresar en término matemáticos.
Dejemos a un lado los “límites” y comencemos con cuestiones más sencillas como la expresión "± a" que se lee “más o menos a ” y quiere decir que "a" es positivo o que "a" es negativo, es muy usada en los resultados de raíces cuadradas, como por ejemplo √(121 )= ±11. También suele usarse para radicales con índice par, o sea, raíces cuartas, raíces sextas así sucesivamente. ¿puedes explicarte el por qué?

Sabiendo que los números son “infinitos” no podemos pasar por alto a las notaciones + ∞ y -∞ (mas infinito y menos infinito) que simbolizan un comportamiento de los números cuando tienden a valores muy “altos o grandes” o muy “bajos o pequeños”.
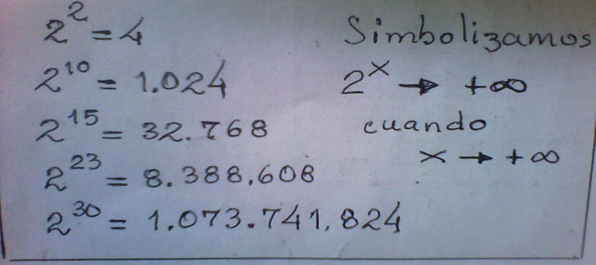
Y con los números, es seguro que nos hemos encontrado con situaciones en donde se requiere aproximar cantidades, es allí donde podemos usar "≅" que se lee “aproximadamente igual a” por ejemplo 23,456 ≅ 23,5 pero en geometría decimos “es congruente a”, así ∆ABC ≅ ∆DEF (el triángulo ABC es congruente al triángulo DEF; eso significa que los triángulos cuando se superponen uno con otro, coinciden), también empleamos "≈" que es “casi igual a”, o “asintóticamente igual a” para el comportamiento numérico de funciones en sus gráficas, así por ejemplo e^(-x) ≈0 cuando x toma valores “muy altos”.
Por otra parte, en las relaciones que son de equivalencias usamos "≡" para simbolizar que una expresión es “equivalente a” otra, por ejemplo la relación “congruencia módulo n”
x ≡y (mod(n)) que se define como "n divide a (x-y)"
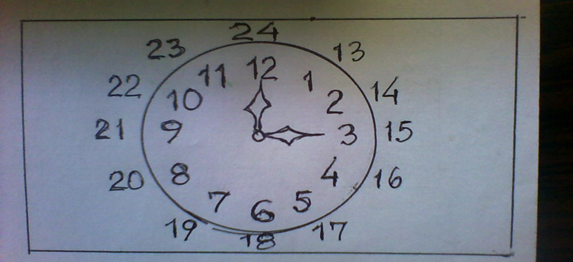
Esta relación la podemos ver en los relojes que expresan las horas a.m. y p.m. con las 24 horas, por ejemplo;
15 ≡3 (mod(12)) equivale a decir 12 divide a (15-3), o sea, 12 divide a (12), lo cual es cierto, entonces esto es que la hora 15 equivale a las 03:00 pm.
¿Qué significaría 20 ≡8 (mod(12)) en relación a las horas?
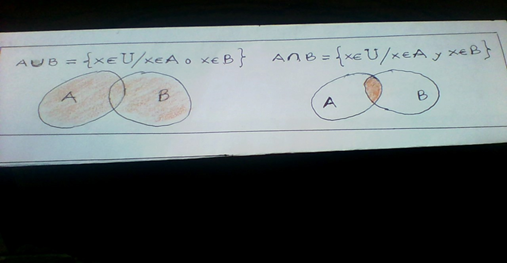
Cuando se está “trabajando” con conjuntos, para decir que un conjunto no tiene elementos se usa la notación ∅ que se traduce como “vacío”, para unir dos o más conjuntos empleamos "∪" y así A∪B significa “ A unido con B ” mientras que para intersectar dos o más conjuntos usamos "∩" y así A∩B significa “A intersectado con B”
En otro orden de ideas, se presenta un símbolo no muy conocido por muchos; "∴" y es usado para concluir un resultado y/o comentario sobre un razonamiento que se venga haciendo. Por ejemplo; Si hoy es sábado, entonces mañana es domingo. Por lo tanto, es fin de semana.
También está este otro símbolo: “ / ” que no es de fracción sino para traducir “tal que”, el cual es muy usado en definiciones. Por ejemplo, la definición de “intervalo abierto”
(a,b)= {x ∈R ∕ a < x < b }
la expresión de la derecha de la igualdad indica un conjunto expresado “por comprensión”, que en este caso significa “el conjunto de todos los números reales tales que son mayores que a pero menores que b.”

Para finalizar esta sesión, nombramos a “los cuantificadores universales” que son “para todo” y “existe” que se simbolizan, respectivamente, por " ∀ " y " ∃ ", estas notaciones son muy empleadas en conjuntos, por ejemplo;
∀ n ∈N, n+1 > 0 que se lee; “para todo número natural n, su consecutivo es positivo” o más resumidamente: “el consecutivo de todo número natural es positivo”
∃ n ∈N, n-12 < 0 que se lee; “existen números naturales n que al restarle 12 el resultado es negativo”.

Me despido compartiendo esta frase: “Dios hizo los números naturales; todos los demás son obra de los hombres.” citada por el célebre matemático alemán Leopold Kronecker.
… Hasta el próximo encuentro…
Sigo agradeciendo a Dios, a mi esposa y a mis hijos por su apoyo y paciencia. También a ti, porque si has leído hasta aquí, es porque me apoyas.
“Las Matemáticas son el lenguaje con el que el Dios ha escrito el universo”
Galileo Galilei
Buen trabajo con su post, está bien elaborado y trae consigo definiciones matemáticas muy interesantes.
No recuerdo porqué sucedía lo de las raíces con bases pares, creo por lo de los números imaginarios.
Esas últimas dos expresiones no las conocía y no las hubiera podido comprender sin este post. Gracias por compartir esto, saludos!