El objetivo de este post presentar la equivalencia de las potencias con exponentes fraccionarios como una forma de expresar las expresiones radicales y de como se cumplen, en ambos casos, como potencias o como raíces, las propiedades de la potenciación.
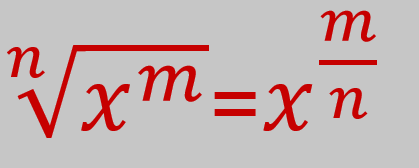
Consideremos la siguiente expresión:
81/3
Aquí vemos la base 8 y el exponente es 1/3
Pero, ¿Cómo hacer con 81/3?
Apriorísticamente podemos usar la calculadora y usar la función potencia así:
Colocar la base 8 y elevarla a la 1/3 colocando el 1/3 entre paréntesis, y así nos da el resultado 2.
Pero, ¿como interpretar la expresión
81/3
En plan de interpretarla voy a utilizar los criterios de una ecuación, es decir, voy a igualar dicha expresión a una variable x, así:
81/3=x
Con el objetivo de eliminar el exponennte 1/3, elevaremos a ambos lados de la igualdad al exponente 3, así:
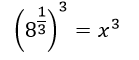
Se va a utilizar una propiedad de la potenciación que se denomina ''potencia de potencia''.
Esta propiedad dice que si se tiene una potencia elevada a otra potencia entonces se debe conservar la base y multiplicar los exponentes, esto es:
(xn )m=xn.m
Aplicando esta propiedad en la parte izquierda de la igualdad de nuestro ejemplo, queda así:
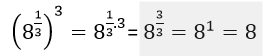
De tal forma que:
8=x3
Luego:
Si 81/3=x entonces 8=x3
Esto se puede generalizar así:
Si y1/n=x entonces y=xn
siendo n diferente de 0.
Continuemos con el ejemplo que venimos desarrollando:

Luego: 23=x3
Para que dos potencias sea iguales deben tener el mismo exponente y la misma base, de tal forma que, en este caso, x debe ser igual a 2.
Sustituyendo x en la ecuación:
81/3=x
Nos resulta:
81/3=2 ya que 23=8
Este resultado puede ser verificado con la calculadora.
A manera de conclusión podemos afirmar que la siguiente expresión:

Veamos algunos ejemplos:
Resuelve las siguientes potencias con exponentes fraccionarios sin usar calculadoras:
91/2
Para resolver sin calculadora, lo primero que se debe hacer es, igualar 91/2, a x, así:
91/2=x
Vemos que 𝑛=2, eso significa que vamos a elevar al cuadrado a ambos miembros de la igualdad con el objetivo de eliminar el exponente 1/2, así:
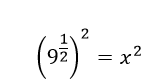
Esto es:
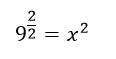
De modo que:
9=x2
Luego convertimos a 9 en potencia, para ello, lo debemos descomponer en producto de sus factores primos:

Y de esta forma, tenemos que:
32=x2
De donde el resultado es: x=3
Puedes verificar este resultado con la calculadora.
Observación
Las potencias con exponentes fraccionarios son equivalentes a una expresión radical de índice n, es decir que:
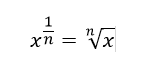
Ejemplo:
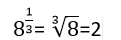
Observe que:
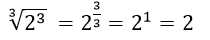
Generalizando, podemos decir que:
De esta manera, la siguiente expresión puede ser resuelta así:
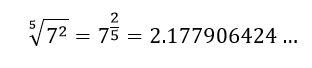
Nota: este resultado fue obtenido con la calculadora.
También se puede afirmar que:
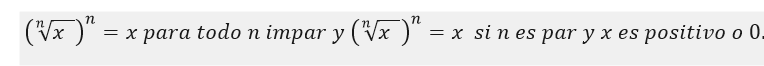
Resolveremos la siguiente ecuación:
(-32)1/5 =x
Para resolver este ejercicio, se expresará el lado izquierdo de la ecuación como una raíz y luego, vamos a elevar a la 5, a ambos miembros de la igualdad, así:
De tal forma que podemos cancelar la raíz así:
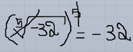
De esta forma, nuestra ecuación queda así:
-32=x5
Descomponiendo 32 como producto de sus factores primos: 32=25
Nuestra ecuación nos queda de la siguiente forma:
-25=x5
Por lo tanto, x=-2
Lo cual corresponde a la solución.
Veamos este otro ejemplo:
Resolver la ecuacion:
(-16)1/2=x
Sigamos el mismo procedimiento del ejemplo anterior.
Elevemos al cuadrado a ambos miembros de la ecuación, así:
[(-16)1/2]2=x2
El 1/2 con el 2 se elimina en el lado izquierdo y la ecuación queda así:
-16=x2
Lo cual es una contradicción, ya que todo número real elevado al cuadrado da como resultado un número positivo.
En consecuencia, este ejercicio no tiene solución.
Pero, si en lugar de tener -16, fuese 16 positivo, el ejercicio sí tiene sentido, ya que cuando la base es positiva se puede aplicar el procedimiento anterior sin problemas para cualquier índice n par.
Veamos:
161/2=x
[161/2]2=x2
16=x2
Pero 16=42
Luego: 42=x2
Finalmente: x=4
A continuación, vamos a colocar unas operaciones variadas con potencias con exponentes fraccionarios o su equivalente en raíces.
Efectúa las siguientes operaciones:
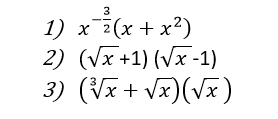
Créditos:
El post es totalmente original de la autora.
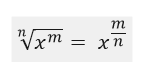
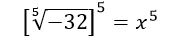
¡Felicitaciones!
Estás participando para optar a la mención especial que se efectuará el domingo 31 de marzo del 2024 a las 8:00 pm (hora de Venezuela), gracias a la cual el autor del artículo seleccionado recibirá la cantidad de 1 HIVE transferida a su cuenta.
¡También has recibido 1 ENTROKEN! El token del PROYECTO ENTROPÍA impulsado por la plataforma Steem-Engine.
1. Invierte en el PROYECTO ENTROPÍA y recibe ganancias semanalmente. Entra aquí para más información.
2. Contáctanos en Discord: https://discord.gg/hkCjFeb
3. Suscríbete a nuestra COMUNIDADEntra aquí para más información sobre nuestro trail. y apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática.
4. Visita nuestro canal de Youtube.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.