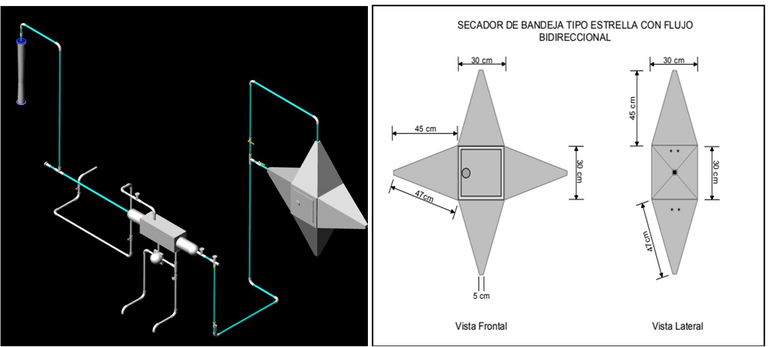
EVALUACIÓN DEL ESPESOR DEL AISLANTE TÉRMICO REQUERIDO EN EL SISTEMA DE SECADO DE BANDEJA TIPO ESTRELLA CON FLUJO BIDIRECCIONAL



CÁLCULOS
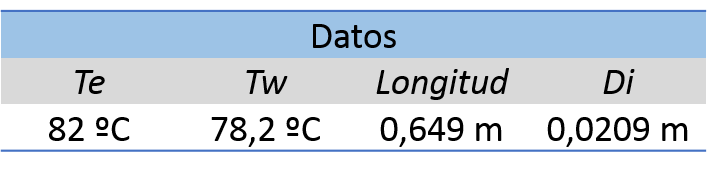
- Determinación del área transversal.
Cuando un sólido geométrico se corta en dos mitades, se expondrá un área. La superficie expuesta, se denomina área de la sección transversal.
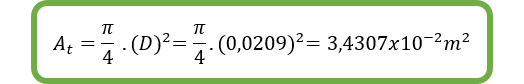
- Determinación del caudal de referencia.
Para este estudio se trabajo a apertura única de rotàmetro de 140mm, por lo cual se uso la siguiente ecuación donde los valores 0.1 y 0.24 son constantes dependientes de la altura del rotàmetro.

- Determinación de la temperatura media.
Representa el promedio aritmético de las temperaturas medias en la admisión y la salida; la cual permanece constante en una sección transversal.

- Determinación de la temperatura de película.
Es el promedio aritmético de las temperaturas de la superficie y del flujo libre. De esta forma, se supone que las propiedades del fluido se mantienen constantes en esos valores a lo largo de todo el flujo.

Una vez obtenida la temperatura de pelicula se determinan las propiedades del Fluido (Aire caliente a 1 atm de presión).
- Determinación del caudal de aire corregido.
Cuando se trabaja en condiciones que no son las correspondientes a las condiciones de trabajo de un equipo medidor de flujo, se realiza una corrección del caudal a través de la siguiente ecuación. Donde el caudal corregido está representado de la siguiente manera, al considerar que las condiciones de trabajo son a presión constante.

- Determinación de la velocidad del fluido.
Se despeja la velocidad de la Ecuación para la determinación del caudal volumetrico y se sustituye.

- Determinación del número de Reynolds.
Las propiedades del aire se evalúan a la temperatura de película, los valores fueron extraídos de la tabla mediante interpolación.

- Determinación del número de Nusselt.
Expresa la relación entre la fricción del fluido y la transferencia de calor para flujo laminar sobre una placa plana.

- Determinación del coeficiente convectivo.
El número de Nusselt representa el mejoramiento de la transferencia de calor a través de una capa de fluido como resultado de la convección en relación con la conducción a través de la misma capa. Entre mayor sea el número de Nusselt, más eficaz es la convección. Un número de Nusselt de Nu=1 para una capa de fluido representa la transferencia de calor a través de ésta por conducción pura.

- Determinación del área superficial de transferencia de calor.
Representa el área superficial de contacto con el fluido. A continuación, se muestran las expresiones utilizadas para distintas configuraciones geométricas.

- Determinación del coeficiente de fricción.
El coeficiente de fricción es un parámetro importante en los estudios de transferencia de calor ya que está directamente relacionado con el coeficiente de transferencia de calor y con los requisitos de potencia del equipo de trabajo. En la mayor parte de los casos se determina de forma experimental y generalmente varía con la ubicación a lo largo de la superficie.

- Determinación del número de Stanton.
Razón de la transferencia de calor en la pared con respecto a la transferencia de calor en la pared por convección. El número de Stanton puede determinarse por distintas analogías, sin embargo, una de las más exactas corresponde a la analogía de Reynolds.

- Determinación de la temperatura real de salida.
Para la determinación de la temperatura de salida real del fluido, se utiliza la siguiente expresión, que se originó a partir de datos experimentales y la relación de distintas analogías que involucran la cantidad de movimiento del fluido por convección y la razón de transferencia de calor de la superficie en cilindros y tuberías.

- Determinación de la diferencia media logarítmica de temperatura.
Se obtiene al seguir el rastro del perfil real de temperaturas del fluido a lo largo de la geometría en estudio y es una representación exacta de la diferencia de temperatura promedio entre el fluido y la superficie.

- Determinación de la pérdida de calor.
La razón de la transferencia de calor por este mecanismo se calcula tomando ciertas consideraciones a la razón de transferencia de calor por convección que se obtiene a través de la ecuación de conservación de la energía.


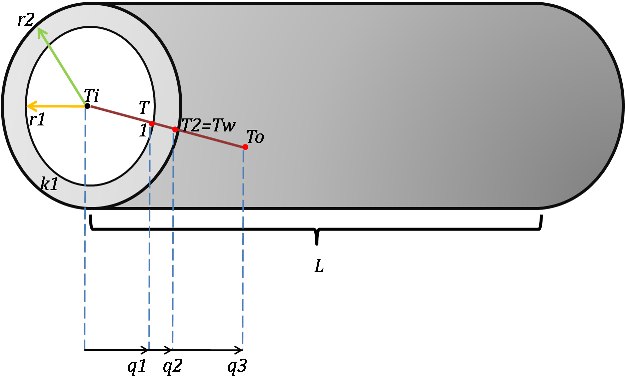
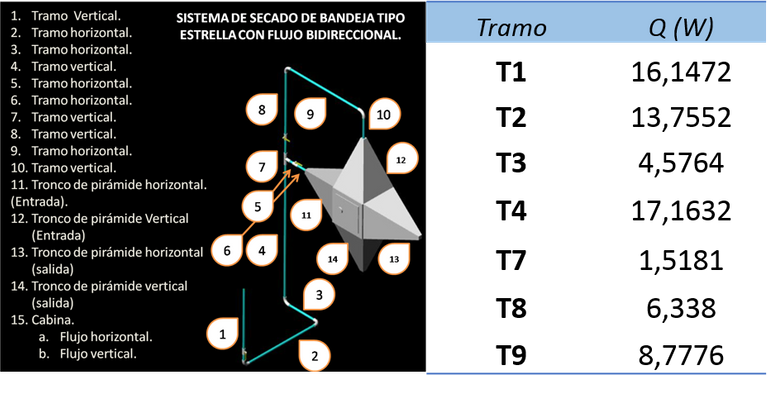
Sistema en estudio.


RESULTADOS
De manera análoga se realizaron los demás calculas de perdida de calor para los diferentes tramos de tuberías a excepción de los tramos 5, 6 y 10, ya que en estos el gradiente de temperatura fue despreciable al igual que su longitud, lo que genero una perdida de calor insignificante. obteniéndose los siguientes resultados:

REFERENCIAS
- Cengel, Yunus A. (2007). Transferencia de calor y masa. Tercera Edición México, Editorial: McGraw-Hill.
- Geankoplis, Christie (1998). Procesos de transporte y operaciones unitarias. México, Editorial: Continental S.A
- J.P. Holman (1986). Transferencia de calor. Editorial: McGraw-Hill.
- Donald Q. Kern (1965). Procesos de transferencia de calor. Editorial: McGraw-Hill.
- Perry, R. H. (1997). Manual del Ingeniero Químico. México: McGraw-Hill.
Agradecido eternamente con usted y con todo el equipo de @cervantes.
Congratulations @benayetfranco! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
SteemitBoard World Cup Contest - Brazil vs Belgium
Participate in the SteemitBoard World Cup Contest!
Collect World Cup badges and win free SBD
Support the Gold Sponsors of the contest: @good-karma and @lukestokes