Ahora bien adentrándonos en el tema, he observado en algunos colegas docentes que la forma más viable y segura que ven para explicarles el concepto de derivada de una función real al alumno es yéndose directamente a la resolución de ejercicios, utilizando directamente las tablas de reglas básicas de derivación para resolver ejercicios donde se le tiene que encontrar la derivada a cualquier función de variable real.
Es una forma que muchos colegas han encontrado para evadir temas abstractos que dentro de la enseñanza resultan bastante difícil para lograr un aprendizaje significativo en el estudiantado, más sin embargo pienso que no es la manera, ya que le resta calidad al aprendizaje.
Lo que propongo es desarrollar un aprendizaje basado en la pasión y profundidad que tengamos al explicar un tópico en específico, con esto buscamos desarrollar el carácter crítico y analítico de aprender del estudiante.
Específicamente el tópico que me apasiona es la forma en como desarrollo en mis clases el concepto de la derivada, como experiencia les comento que el alumnado se entusiasma cuando le formuló la siguiente interrogante:
¿Qué es la derivada?
En la experiencia que tengo como docente, no he tenido algún estudiante que me responda correctamente, todos coinciden en sus respuestas, diciendo como por ejemplo: " es un proceso mediante el cual con una serie de fórmulas resolvemos un ejercicio ". Y no es que ellos tengan la culpa de responder así, el problema esta en como ellos aprenden, ya que muchos docentes de cálculo cuando se disponen a explicar el tema de derivadas, lo primero que hacen es escribir las fórmulas básicas de derivación en el pizarrón, proponer una series de funciones, en muchos casos solo funciones algebraicas y disponerse solamente a resolver ejercicios, haciendo esto que el alumno conciba este concepto como un proceso para resolver un ejercicio.
A partir de este punto es donde entra mi pasión por este tópico esencial del cálculo infinitesimal:
Retrocediendo en el tiempo, nos encontramos dos filósofos y matemáticos como Isaac Newton y Leibniz, los cuales fueron trabajando paralelamente en algo que para su tiempo significa un problema esencial dentro del álgebra y la geometría, donde los conocimientos que se tenían hasta entonces con la geometría de Euclides y los avances de la geometria analitica y algebra no se podían resolver, y no era más que el problema de la Recta Tangente.
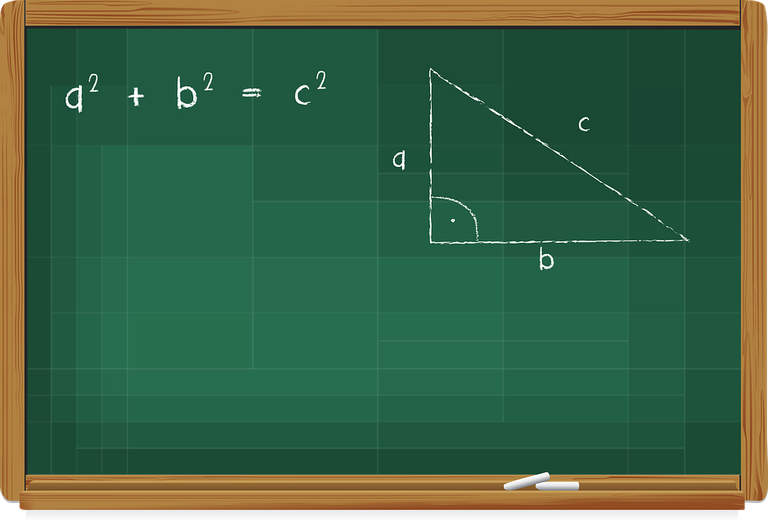
Para encontrar la pendiente de una recta conociendo las coordenadas (x,y) de dos puntos P1 y P2, no existe ningún tipo de problema porque podemos aplicar la siguiente fórmula:
m= Y2-Y1/X2-X1; donde m es la pendiente y (X1,Y1) son los coordenadas del punto 1, y (X2,Y2) son las coordenadas del punto 2.
El problema que se presentó en aquel entonces fue cuando estos dos genios y adelantados en su tiempo pensaron lo siguiente: ¿ Y qué pasa si se tiene que conseguir la pendiente de una recta que es tangente a una función en punto dado ?, el problema ahora nace, es por qué para encontrar la pendiente de la recta tangente a una función en " un punto cualquiera", solo disponemos de un solo punto, y como habíamos visto en explicaciones anteriores, para conseguir la pendiente de una recta necesitamos dos puntos.
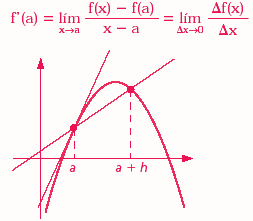
Para ese entonces la solución la encontraron fue en algo que hoy en día conocemos como Límite de una función cuando tiende a un punto, ellos se dispusieron a tomar otro punto arbitrario, y acercarlo tan cerca pero tan cerca al punto tangencial, que este pareciera que fuera un solo punto, y de esta manera poder resolver el problema de la recta tangente.
Lo cual significa que cada vez que estamos resolviendo una derivada por definición que aplicamos la fórmula antes mencionado, lo que estaríamos consiguiendo es el valor de la pendiente (m) que es tangente a cualquier función en un punto dado.
Como reflexión final, les puedo mencionar que aunque parezca algo abstracto, el explicar en este caso el origen de la derivada y darle un concepto bastante práctico de lo que es la derivada de una función, le proporciona alta estima al estudiante para darse cuenta qué el calculo diferencial aparte de ser práctico, también su comprensión depende de dotes analíticos.
Saludos amigos de la comunidad steemit.


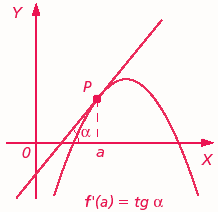
Es un place leer posts de usuarios como tu, que enseñen, que aporten, que den valor añadido a esta red. Gracias por compartir, el equipo Cervantes apoyando a la comunidad.
Es un placer para mi leer comentarios motivadores de parte del gran equipo cervantil, arduo y merecido trabajo, y para recompensar el apoyo, pues me queda esmerarme más y continuar compartiendo contenido para el gusto de mis lectores y seguidores. Saludos
Buen contenido. Espero hagas mas publicaciones asi. 👍
Gracias por el apoyo y el buen comentario. De seguro que sí seguiré complaciendo a mis seguidores con contenidos de esta índole. Saludos
Saludos amigo. Tienes mi voto.
Gracias por el apoyo, de la misma manera te apoyare, saludos.