Difusión, la base de mi tesis, en el cual explique desde un enfoque básico y detallado la teoría fundamental de mi trabajo de investigación, para esta nueva entrega presento la porosidad un concepto simple pero muy importante en relación con los medios porosos.Saludos comunidad científica de steemit, en especial a todos aquellos que publica en el nuevo tags de ciencia #stem-espanol, habilitado por el equipo de @steemstem. Hace 2 meses publique el post
Debemos recordar que un medio poroso es un medio heterogéneo, donde uno de sus componentes es sólido y el otro puede ser gaseoso, líquido u otro estado de la materia, dispuestos de tal manera que el espacio que forma genera "huecos"(fase gaseosa,liquida) entre las partículas o cuerpos que constituyen la fase solida (figura1). Ahora un elemento muy importante en el estudio de los medios porosos es la caracterización de los mismos, lo cual busca una descripción de las propiedades estructurales del medio obteniendo así una información cuantitativa, dentro de esta practica tenemos la porosidad, la superficie especifica, el tamaño de poro, esfericidad entre otros parámetros.
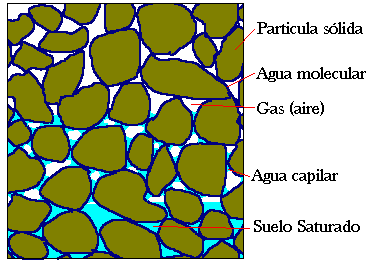
La porosidad es la razón entre el volumen "hueco" y el volumen total de una muestra representativa (VER) de un medio poroso(M.P.), entiéndase el volumen hueco como el espacio formado por la fase fluida. En el estudio de los M.P., la muestra representativa , es un volumen donde se evalúan todos los parámetros mencionados anteriormente y los efectos de transporte que se quieran analizar, cuyo tamaño viene dado por aquel donde las fluctuaciones de la porosidad sean mínimas, es decir, el dominio de los M.P. existe desde regiones microscópicas hasta grandes escalas macroscópicas, y es claro que para pequeñas escalas las variaciones de la porosidad es muy alta, por tanto se requiere entonces de una porción de este medio, donde tales efectos sean despreciables, de manera que este volumen sea una buena representación del medio total que se desea estudiar.
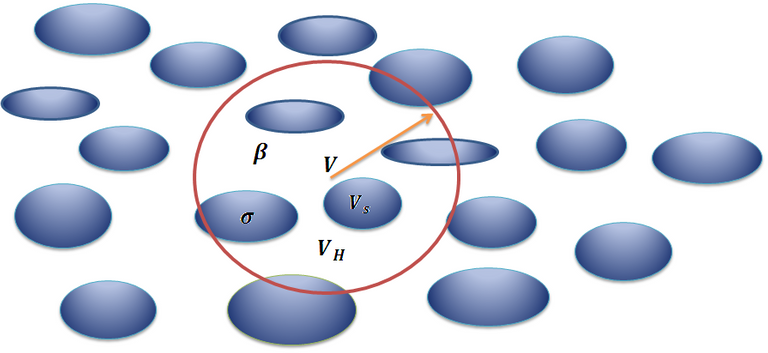
en la figura 2 se muestra un M.P. donde se especifica los siguientes elementos:
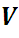 : Volumen total de la muestra, denotado por la circunferencia roja.
: Volumen total de la muestra, denotado por la circunferencia roja.
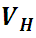 : Es el volumen hueco dentro de la muestra.
: Es el volumen hueco dentro de la muestra.
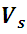 : Volumen de los sólidos dentro de la muestra.
: Volumen de los sólidos dentro de la muestra.
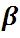 : Fase fluida.
: Fase fluida.
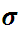 : Fase sólida.
: Fase sólida.
Entonces por definición la porosidad viene dada por:
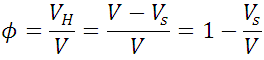
Como ven (1) es una formula muy sencilla, expresa la porosidad como función del volumen del componente sólido, además claramente se puede observar que su máximo valor es 1 en caso de que 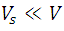 . PAra ver esto mejor desarrollaremos el siguiente ejemplo:
. PAra ver esto mejor desarrollaremos el siguiente ejemplo:
- Consideremos el medio mostrado en la figura 3, una distribución periódica de una partículas cuadradas de lado a, nos interesa conocer la porosidad del medio y ademas obtener una expresión general para el VER del medio
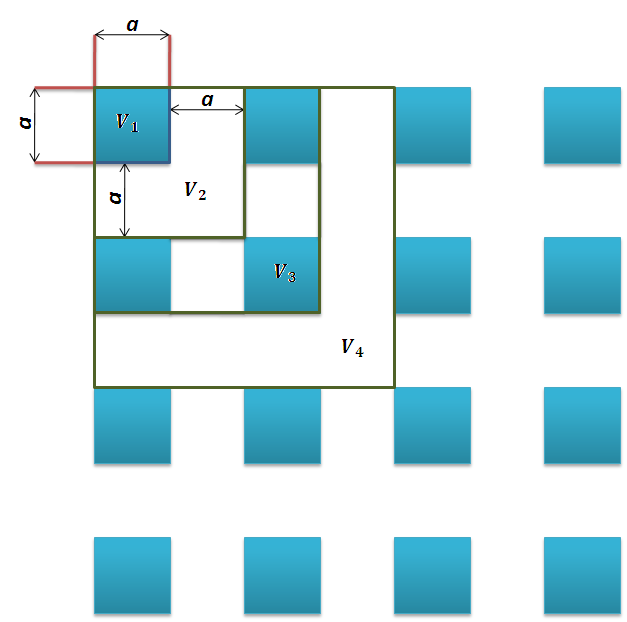
considerando (1), nosotros tomamos volúmenes arbitrarios (este caso en realidad son áreas, pero lo llamaremos volumen, para mantener la nomenclatura) para ver como se comporta la 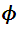 , la forma de hacerlo esta mostrado en la figura 4, por los recuadros marcados en verde, es decir, tomaremos volúmenes cuadrados aumentando en una proporción de lado a, de manera que para
, la forma de hacerlo esta mostrado en la figura 4, por los recuadros marcados en verde, es decir, tomaremos volúmenes cuadrados aumentando en una proporción de lado a, de manera que para 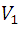 corresponde el primer recuadro, para
corresponde el primer recuadro, para 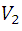 el segundo recuadro y así sucesivamente, para que quede claro mostraremos las primera operaciones:
el segundo recuadro y así sucesivamente, para que quede claro mostraremos las primera operaciones:
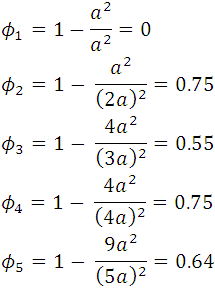
de las operaciones nosotros podemos notar que la porosidad esta en función de las n volúmenes, es decir queda en relación de los valores que toma n, esto se puede apreciar en la siguiente tabla:
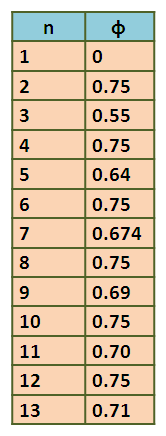
Entonces los valores que toma los n volumenes, arroja una porosidad de 3/4 para los volúmenes donde n es par, y para n par impar, vemos que a medida que aumenta el numero se acerca también a 3/4, entonces de la tabla 1, se puede deducir fácilmente que la porosidad para el medio mostrado en la figura 3 es 3/4, pero la expresión general para nuestro VER lo obtenemos de las relaciones de n con la porosidad de la siguiente manera:
para n par:
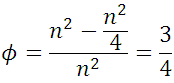
para n impar:
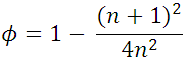
(2) y (3), son las expresiones generales de la porosidad para volumenes de na tomados de la forma como se muestra en la figura 3, ahora si nosotros consideramos los na pequeños como la escala microscópica, entonces a medida que aumente n, nos dirigimos a escalas mayores en la cual sin duda la porosidad es 3/4, esto se puede demostrar hallando el limite de (3), cuando n tiende a infinito.Reescribiendo (3):
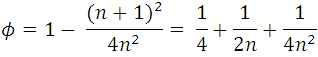
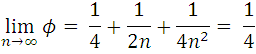
En la siguiente gráfica se puede denotar el comportamiento de la porosidad:
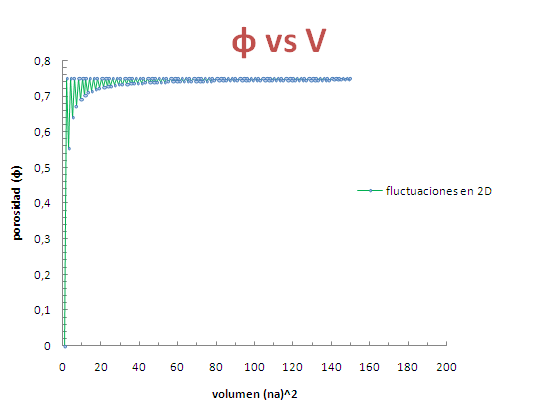
La grafica anterior confirma lo demostrado en la ecuación (4), las fluctuaciones tienden a disminuir para volúmenes donde n es grande, convergiendo a 3/4 como ya lo habíamos deducido.
Veamos otro ejemplo donde tenemos los mismos cuadros, pero esta vez dispuestos en el espacio, es decir,cubos de lado a puestos de manera periódica, como se muestra en la figura 4.
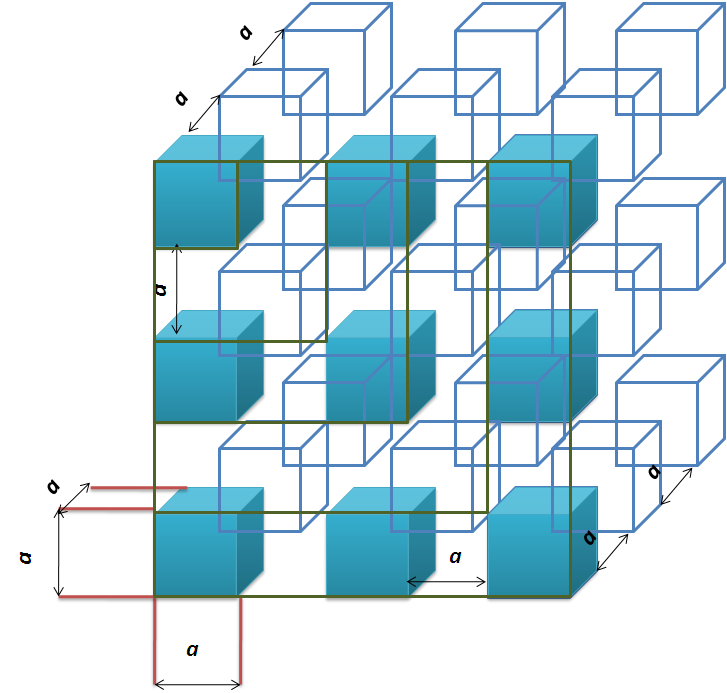
análogo al ejemplo anterior, se toman valores de n volúmenes para obtener la porosidad, en la siguiente tabla se muestran los valores.
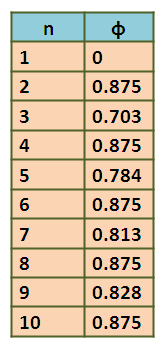
Aqui el valor congruente es 0.875 para los n pares, siguiendo este patrón las expresiones generales para el VER estan dadas por:
Para n par:
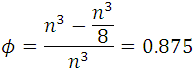
Para n impar:
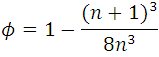
en la siguiente gráfica observamos el comportamiento de la porosidad para este medio.
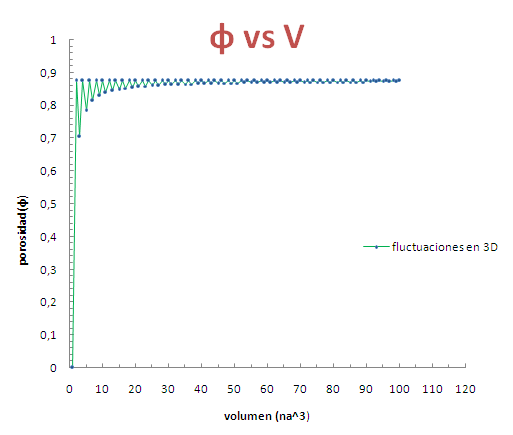
El comportamiento de la porosidad es similar al medio anterior, con un valor de 0.875, un valor mayor y que es de esperase, ya que hay mayor hueco en un espacio tridimensional, que uno bidimensional. Esta pequeña practica corresponde a sola una caracterización de un M.P. idealizado, como son todos los modelados en física, pero que establece un método base para abordar otros casos mas complejos presente en los eventos naturales que nos rodea. Es un gusto poder compartir este pequeño trabajo con ustedes, el cual representa uno de los primeros pasos a realizar en mi trabajo de investigación (para otros medios, claro), espero les interese esta información y no duden en preguntar sobre lo aquí expuesto.
Elaborado por @joseg
referencias:
- Bird, R. B.; Stewart, W. E. y Lightfoot, E. N., 1996. Fenómenos de transporte, Reverté S.A., México D.C., México.
- Dullien, F. A. L. y Batra, V. K., 1970. Determination of structure of porous media. EN: Flow through porous media, American Chemical Society Publications, Washington D.C., EUA, pp. 12-23.
- Torquato, S., 2002. Random Heterogeneous Materials: Microstructure and Macroscopic Properties, Editorial Springer, USA.
Imágenes, tablas y gráficos elaboradas en Power Point y Excel 2007
Esperamos ver detalles de tu trabajo de investigación en otros medios porosos que es un tema muy extenso y que puedes aportar muchísimo con tus discusiones y análisis.Excelente contar con tus publicaciones en la comunidad científica de hablahispana #stem-espanol
Gracias @iamphysical, es un honor y placer poder compartir nuestros conocimientos en nuestro idioma, y ademas que tenga la posibilidad de ser valorados, espero poder seguir contribuyendo con la comunidad científica que publica en #stem-espanol, dándole un buen uso a esta. Saludos de parte de @joseg
Felicidades!

Gracias por el apoyo @carloserp-2000 y al equipo de @steemstem.
excelente!!
Muy productivo y sustancioso tu post, es bueno tener a personas que no traigan buena información y no solo un selfies .. gracias