Hola de nuevo amigos de steemit
En mi publicación anterior he determinado la fórmula de Newton observando lo que sucede en varios casos y llegando a la conclusión de que lo mismo debe suceder en los demás casos. Este método de llegar a una conclusión general por la observación de varios casos particulares se llama método de inducción.
Inducción completa para el Binomio de Newton
Dentro de este método se encuentra la inducción completa, el cual se basa en el siguiente principio:
Si en una serie de casos se puede demostrar que cumpliéndose una propiedad en un caso cualquiera m, tiene que cumplirse en el caso siguiente m+1; y si además se sabe que dicha propiedad se cumple en el primer caso, podemos asegurar que esa propiedad es general, es decir, que se cumple en todos los casos.
Este es el grado de seguridad o nivel exigido por la ciencias exactas, la cual aplicaremos al binomio de Newton a continuación, entonces para el exponente m+1 en el desarrollo de (a+b) se tiene:
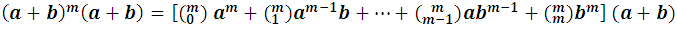
Realizando las multiplicaciones que se indican:
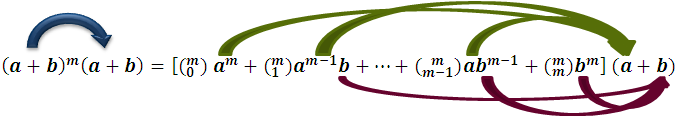
Se puede llegar a:
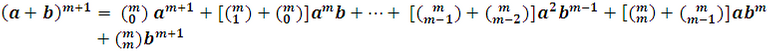
Recordemos que :
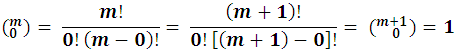
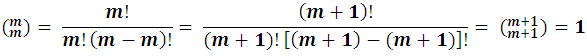
y además:
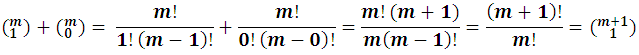
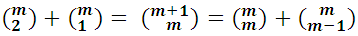
Luego al sustituir estos valores en el desarrollo de los factores (a+b) encontramos:
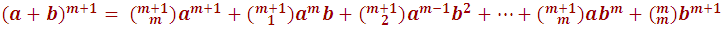
Que es justo la prueba de la generalidad del desarrollo (a+b) con un exponente m+1
Las combinaciones y los coeficientes del binomio
El hecho de que los coeficientes del desarrollo (a+b)m sean precisamente los números:
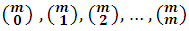
o sea las combinaciones:
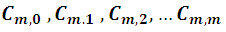
tiene una explicación muy fácil de comprender. En efecto, siendo:
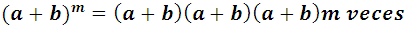
Al multiplicar un solo término de cada paréntesis se forman todas las maneras posible para dicho elemento, por ejemplo:
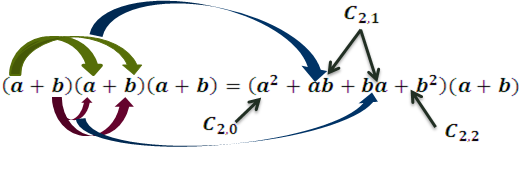
Como se puede observar las combinaciones, son el número de forma posible en la que se puede agrupar los términos, ignorando el orden en lugar de los términos, es decir, es igual decir ab o ba.
Por consiguiente, el término del desarrollo que contenga, por ejemplo, la potencia b4, se obtendrá tomando a B en cuatro de los m paréntesis de todas las maneras posibles, que son Cm,4, y este es, precisamente, el coeficiente de b4 en el término considerado.
Triángulo de Tartaglia o de Pascal
Pascal descubrió muchas propiedades interesantes de los números contenidos en el triángulo, las cuales aparecen en su obra Traité du triangule arithmétique (1665). Antes de Pascal el triángulo figura en las obras de otros matemáticos, tales como Stifel (1544), Peletier (1549) y Tartaglia (1556).
Su formación queda justificada por la propiedad mencionada de los números combinatorios:
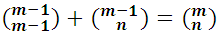
la cual, aplicada a la fórmula del binomio, se expresa diciendo: El coeficiente de lugar n+1 del desarrollo de la potencia (a+b)m es igual a la suma de los coeficientes de los lugares n y n+1 de la potencia (a+b)m-1.
Los coeficientes que aparecen en la fórmula del binomio pueden ser obtenidos para los valores sucesivos de m, mediante un ingenioso artificio. Las filas de números que componen el triangulo siempre comienzan y terminan por 1. Sumando dos números consecutivos de una fila se obtiene el número que figura entre ellos, pero en la fila siguiente:
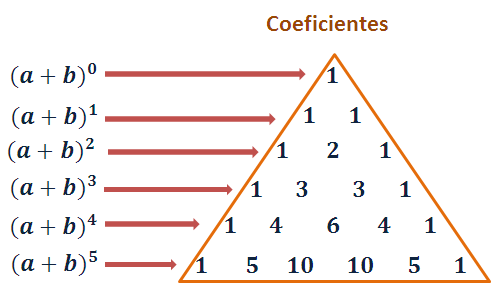
Los números de la primera lateral del triángulo son todos iguales a 1: los de la segunda son los números naturales; los de tercera se llaman números triangulares, y los de la cuarta se llaman números piramidales.
Con esto finalizo estimados steemians, la demostración matemática del binomio de Newton y los fácil que se pueden tener los coeficientes siguiendo el triangulo de Pascal, luego continuo con mas de las simples matemáticas que forman parte importante de la ciencia.
Bibliografía:
by @juancmz